Math Topics
Learning Support
Professional
 Math Methodology is a three part series on instruction, assessment, and
curriculum. Sections contains relevant essays and resources:
Math Methodology is a three part series on instruction, assessment, and
curriculum. Sections contains relevant essays and resources:
Part 1: Math Methodology: Instruction
Part 2: Math Methodology: Assessment essay and resources
Part 3: Curriculum: Content and Mapping and resources
"A student is not a container you have to fill, but a torch you have to light up." --Albert Einstein
"[E]xcellence in teaching is the single most powerful influence on achievement." --John Hattie (2003, p. 4)
 No Child Left Behind
mandated states and districts to adopt programs and
policies supported by scientifically based research. The Every Student
Succeeds Act of 2015 recognized other forms of research in that this law "requires that
states and districts use evidence-based interventions to support school
improvement" (Dynarski, 2015, para. 1; 114th Congress, 2015).
No Child Left Behind
mandated states and districts to adopt programs and
policies supported by scientifically based research. The Every Student
Succeeds Act of 2015 recognized other forms of research in that this law "requires that
states and districts use evidence-based interventions to support school
improvement" (Dynarski, 2015, para. 1; 114th Congress, 2015).
Drawing upon research and an extensive collection of evidence from multiple sources, the Common Core State Standards (2010) were developed to reflect the knowledge and skills that young people need for success in college and careers. Those standards have impacted teachers in several ways, including to guide them "toward curricula and teaching strategies that will give students a deep understanding of the subject and the skills they need to apply their knowledge" (Common Core State Standards Initiative FAQ). For many the standards required changes in curriculum materials and how mathematics is taught, thus they have influenced instructional strategies that educators use.
Unfortunately, since 2010 evidence suggests that the impact of the Common Core State Standards (CCSS) on achievement has been weak, primarily owing to their weak implementation. Per Morgan Polikoff (in Polikoff, Petrilli, & Loveless, 2020) standards implementation has been difficult because "The U.S. system of public education makes implementation of any policy, but especially one that targets the instructional core, close to impossible" (p. 75) and that needs to be fixed. Teachers are receiving too many conflicting messages about classroom approaches (e.g., via "weak instructional supervision, inadequate alignment among policy instruments, and multiple layers of bureaucracy"). He suggests that policy leaders take curriculum more seriously so that teachers won't feel the need to cobble "together curricula from random, unregulated websites" and that they "be given more support to effectively implement their [school district] adopted materials." These latter could come from "a small number of curricular options" selected by the state (p. 75).
It's important to note, however, that the CCSS have had staying power. Although 46 of 50 states originally adopted them, "A lot of states have renamed the standards or even “repealed” them—but in almost every state, what is in place now looks an awful lot like the Common Core as originally written" (Polikoff, Petrilli, & Loveless, 2020, p. 75).
When it comes to student achievement, teachers matter. Your primary goal and role as an educator is to positively affect achievement in all you do. If you become a teacher, you'll soon learn, however, that there are multiple sources of variance in predicting achievement. Per Hattie (2003), "It is what students bring to the table that predicts achievement more than any other variable," accounting for about 50% of that variance (p. 1). This is followed by the influence of teachers, who account for about 30% of that variance. "It is what teachers know, do, and care about which is very powerful in this learning equation" (p. 2). The home, schools (including their principals), and peer effects account for the remaining major sources of variance, about 5-10% each. But, it is excellence in teachers, not just teachers, that makes a difference (Hattie, 2003).
"What teachers know, do, and care about" (Hattie, 2003) can be felt in Alan November's (2016) "7 questions that every new teacher should be able to answer" to be successful in the 21st century. He related each of those to a second question that redefines a teacher's potential added value in changing the culture of a classroom with technology and the internet. In his words:
Various definitions of teaching over time have been proposed and certainly a working definition of the term is needed, if one is to discuss all the challenges involved in teaching. According to Hiebert and Grouws (2007), "Teaching consists of classroom interactions among teachers and students around content directed toward facilitating students’ achievement of learning goals" (p. 372). Further, this definition notes a two-way process and makes teaching "largely under the control of the teacher" (p. 377).
Consider the complexities of teaching as viewed by the National Board for Professional Teaching Standards (NBPTS, 2002):
The fundamental requirements for proficient teaching are relatively clear: a broad grounding in the liberal arts and sciences; knowledge of the subjects to be taught, of the skills to be developed, and of the curricular arrangements and materials that organize and embody that content; knowledge of general and subject-specific methods for teaching and for evaluating student learning; knowledge of students and human development; skills in effectively teaching students from racially, ethnically, and socioeconomically diverse backgrounds; and the skills, capacities and dispositions to employ such knowledge wisely in the interest of students" (NBPTS, 2002, p. 2, What Teachers Should Know section, para. 2).
The NBPTS make it clear that:
This enumeration suggests the broad base for expertise in teaching but conceals the complexities, uncertainties and dilemmas of the work. The formal knowledge teachers rely on accumulates steadily, yet provides insufficient guidance in many situations. Teaching ultimately requires judgment, improvisation, and conversation about means and ends. Human qualities, expert knowledge and skill, and professional commitment together compose excellence in this craft. (NBPTS, 2002, p. 2, What Teachers Should Know section, para. 3).
Ulrich Boser (2019) summed up teaching in another way, stating the "[s]cience of learning principles just don’t seem to be making their way into teacher training or professional development programs" and this "body of knowledge is certainly not the only thing that teachers need to know to teach well."
Teaching is an immensely complex profession. Teachers have to know their discipline well, understand students’ current knowledge base, address behavioral and motivational problems, collaborate with other teachers and administrators on curriculum design, interact with parents, notice signs of potential issues students may be having at home, integrate quantitative and qualitative measures of student learning, and constantly adapt to changing student populations and a changing regulatory environment. (Boser, 2019, Discussion section)
 Bob Sullo, author of
The Motivated Student: Unlocking the Enthusiasm for
Learning (2009), stated that teaching over the past quarter-century has
become more professional due to the emergence of a number of "best practices"
that have significantly affected curriculum and instruction. "A sampling of
innovations includes differentiated instruction, Understanding by Design, the
emergence of state standards, the development of curriculum frameworks,
scope-and-sequence charts that inform teachers of what to teach and when to
teach it, the expanded use of technology in education, active literacy,
curriculum mapping, and the proliferation of professional learning communities.
Formative assessment informs instruction like never before" (Introduction section).
What is striking is that CT4ME includes discussion of many of those innovations
throughout this site.
Bob Sullo, author of
The Motivated Student: Unlocking the Enthusiasm for
Learning (2009), stated that teaching over the past quarter-century has
become more professional due to the emergence of a number of "best practices"
that have significantly affected curriculum and instruction. "A sampling of
innovations includes differentiated instruction, Understanding by Design, the
emergence of state standards, the development of curriculum frameworks,
scope-and-sequence charts that inform teachers of what to teach and when to
teach it, the expanded use of technology in education, active literacy,
curriculum mapping, and the proliferation of professional learning communities.
Formative assessment informs instruction like never before" (Introduction section).
What is striking is that CT4ME includes discussion of many of those innovations
throughout this site.
 The road to incorporating those best practices in teaching is filled with
challenges, as learning to teach is a complex never-ending process. One
might organize that process into four major domains: planning and preparation,
the classroom environment, instruction, and professional responsibilities
(Danielson, 2007). Danielson's work on
Enhancing Professional Practice: A Framework for Teaching,
2nd edition, (2007) is grounded in constructivist theory.
The road to incorporating those best practices in teaching is filled with
challenges, as learning to teach is a complex never-ending process. One
might organize that process into four major domains: planning and preparation,
the classroom environment, instruction, and professional responsibilities
(Danielson, 2007). Danielson's work on
Enhancing Professional Practice: A Framework for Teaching,
2nd edition, (2007) is grounded in constructivist theory.
Regardless of level of experience, teachers always are challenged with how to motivate learners, particularly when you consider the extent of diversity encountered in many schools in the United States. Such diversity involves "understanding that each individual is unique, and recognizing our individual differences." and "knowing how to relate to those qualities and conditions that are different from our own and outside the groups to which we belong, yet are present in other individuals and groups" (Rutgers University, n.d., Diversity and Inclusion Initiatives: About section). Consider that learners and teachers themselves bring to the learning environment a host of variables, such as beliefs, attitudes, perceptions, self-efficacy, motivation, learning styles, habits of mind, cultural influences and demographics (e.g., male/female, sexual orientation, ethnicity, ability/disability, socio-economic status, religion/spirituality, etc.). It is certainly helpful for teachers to be aware of their personal biases, beliefs, and attitudes, as those influence interactions with learners. Also beware of stereotyping, a cognitive bias, as it is assigning characteristics to individuals without knowing anything about them.
It is also important to note Hiebert and Grouws (2007) who stated, "Characteristics of teachers surely can influence their teaching, but these characteristics do not determine their teaching. Teachers with different characteristics can teach in essentially the same way and vice versa" (p. 377).
 Often teachers come into the profession with a conviction that they really will help learners and
are prepared to do so, only to shortly change that conviction to a hope to
help learners. According to Jane Pollock (2007) in
Improving
Student Learning One Teacher at a Time, teachers need to make that hope a certainty by adhering to a Big Four approach, which means
Often teachers come into the profession with a conviction that they really will help learners and
are prepared to do so, only to shortly change that conviction to a hope to
help learners. According to Jane Pollock (2007) in
Improving
Student Learning One Teacher at a Time, teachers need to make that hope a certainty by adhering to a Big Four approach, which means
The Big Four is just the tip of the iceberg. Teachers also accept responsibility for student success, develop communities of respect, and help students become partners in their own success. They take on three instructional roles: direct instructor, facilitator, and coach (Tomlinson & McTighe, 2006). Their professional responsibilities include reflecting on their own teaching, maintaining accurate records, communicating with families, participating in professional communities, growing professionally in content and pedagogical skills, and showing professionalism with their own integrity and ethical conduct (Danielson, 2007, ch. 1).
The fundamental challenges of the teaching profession are also well-articulated in Connecticut's 2010 Common Core of Teaching, which includes "six domains and 46 indicators that identify the foundational skills and competencies that pertain to all teachers, regardless of the subject matter, field or age group they teach" (p. 2). They are useful for teacher preparation programs, beginning teachers, and experienced teachers. For example, among professional responsibilities, the Connecticut Department of Education (2010) indicated "Continually engaging in reflection, self-evaluation and professional development to enhance their understandings of content, pedagogical skills, resources and the impact of their actions on student learning" (p. 10). Collaboration and proactive communication with colleagues, administrators, students, and families are featured elements, as are understanding the legal rights of individuals with disabilities, and the role that race, gender, and culture might have on professional interactions with students, families, and colleagues, and ethical uses of technology.
 Thus, teachers are challenged to know and communicate subject matter; to design curriculum, instruction, and assessments; to be knowledgeable about diverse
student populations, to be knowledgeable about effective uses of data (e.g., see
How Teachers Can Turn Data into Action
by Daniel Venables, 2014) and technology, to conduct action research to improve their practice, to
implement existing research, and to be learner-centered in their approach.
On top of all this is the need to continually grow in the profession, maintain sanity, minimize stress,
learn from mistakes, and let us not forget--prepare students for
standardized testing.
Thus, teachers are challenged to know and communicate subject matter; to design curriculum, instruction, and assessments; to be knowledgeable about diverse
student populations, to be knowledgeable about effective uses of data (e.g., see
How Teachers Can Turn Data into Action
by Daniel Venables, 2014) and technology, to conduct action research to improve their practice, to
implement existing research, and to be learner-centered in their approach.
On top of all this is the need to continually grow in the profession, maintain sanity, minimize stress,
learn from mistakes, and let us not forget--prepare students for
standardized testing.
With all this in mind, Carole Frederick Steele (2009) would add that teachers need to be adept at improvising, interpreting events in progress, testing hypotheses, demonstrating respect, showing passion for teaching and learning, and helping students understand complexity. Fortunately, she reminded us that "No teacher is likely to excel at every aspect of teaching....What experts attend to and ignore is markedly different from what beginners notice. The growth continuum ranges from initial ignorance (unaware) to comprehension (aware) to competent application (capable) to great expertise (inspired)," paralleling Bloom's taxonomy. "Lack of awareness occurs before Bloom's categories. The awareness stage is a fair match for Bloom's stage of knowledge and understanding. Teachers at the capable stage use application and analysis well. Educators who reach the inspired stage have become skilled at synthesis and evaluation in regard to their thinking about teaching and learning" (Introduction section).
Teaching experience matters (Kini & Podolsky, 2016). "What distinguishes the beginning from the accomplished teacher is the degree of sophistication in the application of the knowledge and skills" (Council of Chief State School Officers, 2011, p. 8). However, years of experience does not equate to being an expert. From a review of literature and a synthesis of over 500,000 studies on differences between experience and expertise in teaching, Hattie and colleagues (2003) identified five major dimensions illustrating the expertise of excellent teachers and then elaborated on 16 attributes within those. Expert teachers:
W. James Popham (2009) summed up the nature of teaching in the 21st century. He stated, "once we strip away its external complexities, teaching boils down to teachers' deciding what they want their students to learn, planning how to promote that learning, implementing those plans, and then determining if the plans worked" (Preface section, para. 7).
Resources on the current page will assist you with your knowledge of students and instructional practices. CT4ME's section on Professional Development includes a variety of resources to assist you with becoming more knowledgeable about the mathematics content you teach and how to enhance your teaching skills. Our section on Standardized Test Preparation provides solid advice and resources. Technology Integration will assist you with strategies for incorporating technology into your instruction, including designing your classroom web site, and incorporating multimedia into math projects. You can learn more about scientifically based research and action research at our Education Research section.
 Dimensions of Learning
(Marzano & Pickering, 1997) is an instructional framework based on five
types of thinking, called the dimensions of learning, that are considered essential to student learning and academic
performance:
Dimensions of Learning
(Marzano & Pickering, 1997) is an instructional framework based on five
types of thinking, called the dimensions of learning, that are considered essential to student learning and academic
performance:
Source: Marzano, R., & Pickering, D. (1997). Dimensions of learning teacher's manual (2nd ed.). Alexandria, VA: ASCD.
 According to Art Costa (n.d.), "A "Habit of
Mind” means having a disposition toward behaving intelligently when
confronted with problems" (para. 2). Such habits include, but are not limited to
the following:
According to Art Costa (n.d.), "A "Habit of
Mind” means having a disposition toward behaving intelligently when
confronted with problems" (para. 2). Such habits include, but are not limited to
the following:
Source: Costa, A. L. (n.d.). Describing 16 habits of mind. https://www.habitsofmindinstitute.org/about-us/hear-art/
Costa and Kallick (2008) elaborate on this topic in Learning and Leading with Habits of Mind: 16 Essential Characteristics for Success
 Art Costa, Robert Garmston, and Diane Zimmerman (2012) defined
five states of mind that "create a growth mindset that is a potent
force for fostering collective excellence and influencing,
motivating, and inspiring our intellectual capacities." They include the drive for
efficacy, the drive for consciousness (reflection on one's actions
and those of others), the drive for flexibility, the drive for
craftsmanship, and the drive for interdependence. Effective
teachers demonstrate those dispositions.
Art Costa, Robert Garmston, and Diane Zimmerman (2012) defined
five states of mind that "create a growth mindset that is a potent
force for fostering collective excellence and influencing,
motivating, and inspiring our intellectual capacities." They include the drive for
efficacy, the drive for consciousness (reflection on one's actions
and those of others), the drive for flexibility, the drive for
craftsmanship, and the drive for interdependence. Effective
teachers demonstrate those dispositions.
Source: Costa, A., Garmston, R., & Zimmerman, D. (2012, November 8). What mind-sets drive teacher effectiveness? ASCD Express, 8(3). http://web.archive.org/web/20150509012230/http://www1.ascd.org/ascd-express/vol8/803-costa.aspx
 Carol Dweck, author of
Mindset: The New Psychology of Success
(2007), coined the terms fixed mindset and growth mindset.
When students and educators have a growth mindset, they understand
that intelligence can be developed. Students focus on improvement
instead of worrying about how smart they are. They work hard to
learn more and get smarter. Through years of research, she and
colleagues have found that students who learn this mindset show
greater motivation in school, better grades, and higher test scores
(Mindset Works
website, The Science section).
Carol Dweck, author of
Mindset: The New Psychology of Success
(2007), coined the terms fixed mindset and growth mindset.
When students and educators have a growth mindset, they understand
that intelligence can be developed. Students focus on improvement
instead of worrying about how smart they are. They work hard to
learn more and get smarter. Through years of research, she and
colleagues have found that students who learn this mindset show
greater motivation in school, better grades, and higher test scores
(Mindset Works
website, The Science section).
Dweck is also author of Mindsets and Math/Science Achievement (2008), an article prepared for the Carnegie Corporation of New York-Institute for Advanced Study. She provided evidence that mindsets "can predict math/science achievement over time" and "can contribute to math/science achievement discrepancies for women and minorities." Further, "interventions that change mindsets can boost achievement and reduce achievement discrepancies; and educators play a key role in shaping students’ mindsets" (p. 2).
Caution: In revisiting growth mindset, Dweck (2015) cautioned that misinterpretations of mindset concepts can actually harm students by perpetuating the failed self-esteem movement. "A growth mindset isn’t just about effort. Perhaps the most common misconception is simply equating the growth mindset with effort. Certainly, effort is key for students’ achievement, but it’s not the only thing. Students need to try new strategies and seek input from others when they’re stuck. They need this repertoire of approaches—not just sheer effort —to learn and improve" (para. 5). So, mindset concepts are not about praising students' effort just to make them feel good, even if they are not learning. "The growth mindset was intended to help close achievement gaps, not hide them. It is about telling the truth about a student’s current achievement and then, together, doing something about it, helping him or her become smarter" (para. 7).
Caution: Research on growth mindset has mixed reviews on its effectiveness. Citing the research, the Advocates for the Science of Math (2021b) addressed the misconception that a growth mindset increases math achievement. They stated: "Intervention research on stand-alone growth mindset interventions yield minimal gains on GPA in mathematics courses and replication attempts have failed. The most effective way to improve academic achievement is to deliver skill-building intervention."
Harry Fletcher-Wood (2022) addressed this issue in his article, Is growth mindset real? New evidence, new conclusions and posed the following question: "How can robust studies show having a growth mindset makes no difference – and then a robust study show that encouraging a growth mindset makes a difference?"
Also consider:
Burgoyne, A. P., Hambrick, D. Z., & Macnamara, B. N. (2020). How firm are the foundations of mind-set theory? The claims appear stronger than the evidence. Psychological Science, 31(3), 258-267.
Their "results suggest[ed] that the foundations of mind-set theory are not firm and, in turn, call into question many assumptions made about the importance of mind-set. Given the public spotlight on mind-set, it may be prudent for mind-set researchers to temper strongly worded claims" (p. 9).
Researchers at the University of Esssex in the UK (Sparks, 2019) noted the following approaches shown to encourage a student's growth mindset in math:
CueThink is one tool designed "to foster a growth mindset and empower students to see challenges as opportunities." It is presented as "an innovative application and a pedagogy focused on improving critical thinking skills and math collaboration for students in grades 2-12." This tablet and web-based product "captures and presents the thinking process and cognition." Students create a video vignette of their solutions, post to a gallery, and receive feedback from peers and their teacher, thus making math social. George Polya's four-step problem solving method is used: understand, plan, solve, and review.
 In
Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching,
Jo Boaler (2016) elaborated on how educators can teach math
better so as to promote a growth mindset. She expands her
ideas on "paying attention to the math questions and tasks that
students work on, the ways teachers and parents encourage or grade
students, the forms of grouping used in classrooms, the ways
mistakes are dealt with, the norms developed in classrooms, the math
messages we can give to students, and the strategies they learn to
approach math" (p. xiii).
In
Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching,
Jo Boaler (2016) elaborated on how educators can teach math
better so as to promote a growth mindset. She expands her
ideas on "paying attention to the math questions and tasks that
students work on, the ways teachers and parents encourage or grade
students, the forms of grouping used in classrooms, the ways
mistakes are dealt with, the norms developed in classrooms, the math
messages we can give to students, and the strategies they learn to
approach math" (p. xiii).
Class Dojo: Ideas has a video series on developing a growth mindset, which was created in collaboration with Carol Dweck. It is meant for young learners. Explore this big idea with animated characters, Mojo and Katie.
Mindset Works has resources, teaching strategies, and how to promote mindset in your school. See free resources.
The Mindset Kit, produced by PERTS (Project for Education Research That Scales) at Stanford University is "a free, online resource designed to help educators and parents learn about adaptive academic mindsets, learn practices that promote these mindsets, and download activity ideas" (PERTS description). Note: There are a series of Learnstorm Growth Mindset Actitivies for elementary and high school learners posted on Khan Academy. These were developed in partnership with PERTS.
Youcubed at Stanford University promotes a growth mindset with teaching ideas, a searchable database of tasks, and videos (e.g., number talks, brain science, enquiry based learning, etc.). The site includes a Mathematical Mindset Teaching Guide designed "to help teachers create or strengthen a growth mindset culture. This guide contains five Mathematical Mindset Practices along with links to teaching videos."
Daniel Willingham, a cognitive scientist, addressed this question in his American Educator article (Winter 2009-2010): Is It True That Some People Just Can't Do Math? His response:
"While it is true that some people are better at math than others -- just like some are better than others at writing or building cabinets or anything else -- it is also true that the vast majority of people are fully capable of learning K-12 mathematics. Learning mathematics does not come as naturally as learning to speak, but our brains do have the necessary equipment. So learning math is somewhat like learning to read: we can do it, but it takes time and effort, and requires mastering increasingly complex skills and content. Just about everyone will get to the point where they can read a serious newspaper, and just about everyone will get to the point where they can do high-school level algebra and geometry -- even if not everyone wants to reach the point of comprehending James Joyce's Ulysses or solving partial differential equations" (p. 14).
Living Proof: Stories of Resilience Along the Mathematical Journey was published by the American Mathematical Society and the Mathematical Association of America in 2019. It begins by noting "Somehow, when we encounter difficulties in mathematics, our natural tendency is to retreat, to think it’s too hard, we’re not smart enough, or we’re not “math people." .... There are no such people. People who succeed in mathematics, like people who learn a musical instrument or a new language, spend a lot of time not understanding and feeling frustration. The path to understanding in mathematics necessarily involves, in the words of Steve Klee, being “willing to struggle.’’ It is strange that people do not understand this about mathematics when it is commonplace in essentially every other field of human endeavor’’ (p. v).
"The ability to succeed in a mathematical program should not be hindered by a person’s gender, race, sexuality, upbringing, culture, socio-economic status, educational background, or any other attribute" (p. ix). So, in this ebook, freely available online, you'll read the stories of success and struggle from real people who took on the challenge of learning mathematics. You'll also get insight into a wide range of careers involving mathematics.
 Gaining confidence in teaching takes time, and requires goal
setting, reflection, dialogue and collaboration among colleagues. Three goals
are essential for success:
Gaining confidence in teaching takes time, and requires goal
setting, reflection, dialogue and collaboration among colleagues. Three goals
are essential for success:
 New teachers, and even those with experience, will benefit from
Smart from the Start: 100 Tools for
Teaching with Confidence by James Stronge, Jessica Straessle, and
Xianxuan Xu (2023). This book addresses the goals above and delves into six major teaching concerns:
ways to begin the school year with setting up your classroom and
establishing rules and procedures, classroom management, instructional
planning, student engagement, assessment, and your well-being as a teacher.
New teachers, and even those with experience, will benefit from
Smart from the Start: 100 Tools for
Teaching with Confidence by James Stronge, Jessica Straessle, and
Xianxuan Xu (2023). This book addresses the goals above and delves into six major teaching concerns:
ways to begin the school year with setting up your classroom and
establishing rules and procedures, classroom management, instructional
planning, student engagement, assessment, and your well-being as a teacher.
The American Psychological Association, Coalition for Psychology in Schools and Education (2015) identified the top 20 principles from psychology "that would be of greatest use in the context of preK–12 classroom teaching and learning" (p. 3). Two of those address classroom management:
Classroom management plays a significant role in effective teaching and ultimate achievement of learners. It occurs at two levels--what can be seen in the classroom during actual contact with learners, and what goes on "behind-the-scenes" outside of the classroom. The latter would typically include planning and follow-up activities that teachers do in connection with classroom management.
Per Kratochwill (n.d., Introduction section), "Although there is no agreed-upon definition of classroom management, the framework offered by Evertson and Weinstein (2006) represents a current and widely accepted view. According to Evertson and Weinstein, classroom management has two distinct purposes: “It not only seeks to establish and sustain an orderly environment so students can engage in meaningful academic learning, it also aims to enhance student social and moral growth” (p. 4). It's more than organizing the physical space for student safety and easy access to materials. It's more than deciding how you will manage classroom procedures, instructional groups and student behavior. It means creating a classroom environment of respect and rapport, and a culture for learning (Danielson, 2007, ch. 1).
In terms of enhancing a culture of learning, technology can also assist teachers in planning and managing tasks they typically do, including communicating with parents. Teachers can use online calendars and to-do lists and online lesson planning tools. Rather than making multiple copies of class handouts, they can post a single copy to a class website. They can use online grade books and grading tools. Technology enables them to create assessments with a variety of apps, and to provide individualized feedback to electronic documents/assignments submitted by their learners. They can even use technology to manage the noise level in the classroom.
Teachers should we aware of four principles on what motivates students. According to the American Psychological Association, Coalition for Psychology in Schools and Education (2015):
In an effective classroom environment, Sullo (2009) indicated that there is no fear factor, which some teachers themselves invoke just by their tone and what they say in reaction to learners' deeds and actions. Sometimes teachers are not even aware of the affect their sarcasm and negativism might have on motivation. In a culture of success, the teacher's message should be "This is important. You can do it. I won't give up on you" (Ch. 2, Getting Started section).
Teachers know how to internally motivate learners, rather than relying on external motivators as coercions and rewards/punishments that do not work for the majority of learners. A key factor in motivation is to engage learners emotionally.
In fact, students are internally driven by the needs built into their genetic code, and they behave in a never-ending quest to satisfy the universal needs to connect, be powerful, make choices, and have fun in a safe, secure environment. Our success as teachers is largely determined by how effective we are at creating learning environments where students can meet their needs by immersing themselves in the academic tasks we provide. (Sullo, 2009, Ch. 3, Basic Needs section)
To have students truly self-motivated, Mike Anderon (2021) stated that teachers must leverage six intrinsic motivators: autonomy (self-direction), belonging, competence, purpose, fun, and curiosity. He illustrated that autonomy can be enhanced by giving students choices to demonstrate their understanding. Collaborative learning structures enhance belonging. However, direct instruction and guided practice are also needed to build social skills, not just academic skills. Differentiation (e.g., via assignments, demonstrations of learning, or tasks to complete) enhances competence. As to purpose, learners might find the purpose of some activities as obvious (e.g., project-based or service learning). But, if not obvious to learners, give them a reason that matters to them in the moment. A little fun goes a long way to enhance social competence, confidence, self-regulation, and more. For example, games that enhance instructional content or having students create their own games aligned to content add fun. Curiosity is enhanced when work can be linked to students' interests (e.g., independent research projects).
 Everyone, regardless of ability, will most likely encounter frustrations and
failures at some point in life. Their motivation, learning, and success
will be affected by how well they are able to respond to such experiences.
Saying "you can do this" is important, but how should educators "teach the
virtues of grit--tenacity, perseverance, and the ability to never give
up" (Hoerr, 2013, Why Grit? section). Thomas Hoerr addressed this issue in
Fostering Grit: How do I prepare my students for the real world?
and provided six steps of teaching for grit:
Everyone, regardless of ability, will most likely encounter frustrations and
failures at some point in life. Their motivation, learning, and success
will be affected by how well they are able to respond to such experiences.
Saying "you can do this" is important, but how should educators "teach the
virtues of grit--tenacity, perseverance, and the ability to never give
up" (Hoerr, 2013, Why Grit? section). Thomas Hoerr addressed this issue in
Fostering Grit: How do I prepare my students for the real world?
and provided six steps of teaching for grit:
Hoerr (2013) recognized that implementation of the above steps "varies according to grade, subject matter, and each student's individual ability, but the steps themselves are consistent" (The Six Steps section).
 In
Emotions,
Learning, and the Brain: Exploring the Educational Implications of Affective Neuroscience, Mary Helen Immordino-Yang (2016)
linked motivation to emotions, stating "for school-based learning to have any hope of
motivating students, of producing deep understanding, or of transferring into
real-world skills--all hallmarks of meaningful learning, and all essential to
producing informed, skilled, ethical, and reflective adults--we need to find
ways to leverage the emotional aspects of learning in education" (p. 18).
Further, "Even in academic subjects that are traditionally considered
unemotional, such as physics, engineering, or math, deep understanding depends
on making emotional connections between concepts" (p. 19). She proposed
three strategies that teachers might use to help learners develop emotional
thought in classroom learning:
In
Emotions,
Learning, and the Brain: Exploring the Educational Implications of Affective Neuroscience, Mary Helen Immordino-Yang (2016)
linked motivation to emotions, stating "for school-based learning to have any hope of
motivating students, of producing deep understanding, or of transferring into
real-world skills--all hallmarks of meaningful learning, and all essential to
producing informed, skilled, ethical, and reflective adults--we need to find
ways to leverage the emotional aspects of learning in education" (p. 18).
Further, "Even in academic subjects that are traditionally considered
unemotional, such as physics, engineering, or math, deep understanding depends
on making emotional connections between concepts" (p. 19). She proposed
three strategies that teachers might use to help learners develop emotional
thought in classroom learning:
 Marzano, Marzano, and Pickering (2003), authors of
Classroom management that works: Research-based
strategies for every teacher, conducted a meta-analysis of
100 reports on this issue, addressing four general components of
effective classroom management: rules and procedures, disciplinary
interventions, teacher-student relationships, and mental set. This
latter refers to an ability to remain emotionally objective and
businesslike and "to identify and quickly act on potential behavioral
problems" (p. 75). They found "on the average, students in classes where
effective management techniques are employed have achievement scores
that are 20 percentile points higher than students in classes where
effective management techniques are not employed" (p. 10).
Marzano, Marzano, and Pickering (2003), authors of
Classroom management that works: Research-based
strategies for every teacher, conducted a meta-analysis of
100 reports on this issue, addressing four general components of
effective classroom management: rules and procedures, disciplinary
interventions, teacher-student relationships, and mental set. This
latter refers to an ability to remain emotionally objective and
businesslike and "to identify and quickly act on potential behavioral
problems" (p. 75). They found "on the average, students in classes where
effective management techniques are employed have achievement scores
that are 20 percentile points higher than students in classes where
effective management techniques are not employed" (p. 10).
Bob Sornson (2010) provided tips, which fall within those four components, for creating a positive classroom environment that will enhance student achievement:
In terms of Sornson's tip on offering choices, Bryan Goodwin (2010) reminded educators that while research suggests that students be given choices, the number of choices should be limited. Less experienced students might be offered fewer choices, perhaps just two, while more advanced students might gradually be given from three to five options. When learners have too many choices, they might spend too much time making the choice and be less satisfied in that choice at the expense of completing work with quality. There is also risk that their motivation to do a good job might decrease, if they've spent their mental energy making the choice and then worry if it was the right one.
And in terms of setting high expectations for all, Robert Marzano (2010) reminded educators that this is easier said than done. It's the "teachers' behaviors toward students [that] are much more important than their expectations," as students "make inferences on the basis of these behaviors" (pp. 82-83). Students become easily aware of differences, as "teachers tend to make less eye contact, smile less, make less physical contact, and engage in less playful or light dialogue" with low-expectancy students. They also pose fewer and less challenging questions to them, and delve into their answers less deeply and reward them for less vigorous responses" (p. 83). The key to overcome this is for teachers to be aware of their own behaviors: identify students as early as possible for whom they have low expectations, identify their similarities and differential treatment of them, and then set out to change and treat low-expectancy and high-expectancy students the same.
Teachers can demonstrate positive behaviors to influence students' perceptions, as those perceptions have a great deal to do with effective instruction. Echoing Sornson (2010), Marzano (2011) stated that developing positive perceptions involves teachers showing interest in students' lives, advocating for students with such actions as the appearance of wanting students to do well and providing assistance to that end, never giving up on students, and acting friendly. "With good relationships in place, all other instructional strategies seem to work better" (p. 82).
 Diversity plays a significant role in classroom management.
Disabilities and cultural differences impact behavioral differences.
It important to know the nature of a disability. For example, an
autistic child might require consistency in his/her schedule as
disruptions in routine might trigger inappropriate behaviors. In responding to students with
disabilities, some learners might need individualized plans for behavior
management. Ideas might be to develop a behavior progress
monitoring form with categories such as "Brought supplies, Worked
productively, Was respectful of others" for various time frames (e.g.,
periods in a school day) or to develop a behavioral contract. In
terms of cultural differences, teachers and all learners in a class
should be aware of each others' interaction styles. What is
acceptable in one culture might not be in another. For example, there are cultural
differences in what is acceptable in speaking to others (e.g., one at a
time, and loud voice), levels of physical activity and verbal discourse
needed with thinking and learning, attitudes about sharing and
respecting physical space, authority figures, what constitutes an
authority figure and the manner in which deference is shown to authority
figures (Voltz, Sims, & Nelson, 2010, pp. 52-55). Voltz, Sims,
and Nelson authored Connecting teachers,
students, and standards: Strategies for success in diverse and inclusive
classrooms (2010).
Diversity plays a significant role in classroom management.
Disabilities and cultural differences impact behavioral differences.
It important to know the nature of a disability. For example, an
autistic child might require consistency in his/her schedule as
disruptions in routine might trigger inappropriate behaviors. In responding to students with
disabilities, some learners might need individualized plans for behavior
management. Ideas might be to develop a behavior progress
monitoring form with categories such as "Brought supplies, Worked
productively, Was respectful of others" for various time frames (e.g.,
periods in a school day) or to develop a behavioral contract. In
terms of cultural differences, teachers and all learners in a class
should be aware of each others' interaction styles. What is
acceptable in one culture might not be in another. For example, there are cultural
differences in what is acceptable in speaking to others (e.g., one at a
time, and loud voice), levels of physical activity and verbal discourse
needed with thinking and learning, attitudes about sharing and
respecting physical space, authority figures, what constitutes an
authority figure and the manner in which deference is shown to authority
figures (Voltz, Sims, & Nelson, 2010, pp. 52-55). Voltz, Sims,
and Nelson authored Connecting teachers,
students, and standards: Strategies for success in diverse and inclusive
classrooms (2010).
In terms of planning and classroom management, certainly new teachers would benefit from the wisdom of their more experienced colleagues. They and mentors can serve as resources for initial concerns such as "setting up the classroom and preparing for the first weeks of school, covering the required curriculum without falling behind or losing student interest, grading fairly, dealing with parents, and maintaining personal sanity" (Mandel, 2006, p. 67).
Experienced teachers are better able to integrate and draw connections between current, past, and future learning and relate their content to other curricular areas. They tend to be able to better use such classroom management skills as voice, gestures, reading student facial expressions and body language, and proximity. They can see the big picture--in planning they can anticipate problems and a need for alternative plans and adjust their practice accordingly. They also know their students' needs and evaluate their lessons according to students' learning growth--that is they measure effectiveness of a lesson beyond meeting the broad objective of the day. Plus, they are knowledgeable about school and community resources that can benefit students. They understand the culture of the school, and have amassed strategies to effectively engage parents in collaborative activities. They understand how to motivate students and maintain their interest even in the face of temporary failure (NBPTS, 2002).
In the classroom, Marzano et al. (2003) said that it is important to involve students in the design of classroom rules and procedures. Although rules will vary, they should be specific and generally address expectations for behavior, beginning and ending the day or period, procedures for transitioning from one activity to the next, interruptions, materials and equipment, group work, seatwork and teacher-led activities (p. 26).
In fact this involvement of students in the design of classroom rules and procedures is one of the practices of the Responsive Classroom approach to improving interactions with children in elementary school. Some of the practices would also apply well with upper grades. The approach is based on the premise that children learn best when they have both academic and social-emotional skills and is the result of research and thinking from child development and constructivist educators (e.g., Piaget, Gesell, Montessori, Dewey, Erikson, and Vygotsky). As a general approach to teaching, educators might consider the following in which readers will note some of the tips Sornson (2010) also provided:
As a reminder, responsive classroom practices should also include breaks in lessons, such as short energizer activities for the whole group, quiet time, and brain breaks that allow students to move about and interact. Brain breaks also help to increase focus, motivation, learning, and memory (Responsive Classroom web site, 2021).
In summary, when inappropriate behaviors occur, apply the ABC method. Determine the antecedents of the behavior, how the behavior happens, and consequences for the student after the inappropriate behavior occurs. You might be able to help the learner substitute a more appropriate behavior as a result of your assessment (Voltz, Sims, Nelson, 2010, pp. 56-57). Focus on the behavior and not the individual, as misbehavior might have nothing to do with you as the teacher.
 And, if your teaching is not going as well as you'd like and is
affecting the success of your learners, Elizabeth Breaux (2009) might suggest to
consider if you've done any of the following:
And, if your teaching is not going as well as you'd like and is
affecting the success of your learners, Elizabeth Breaux (2009) might suggest to
consider if you've done any of the following:
If you answer is yes to any of the above mistakes, it might be time to make changes in your teaching. Breaux is the author of How the best teachers avoid the 20 most common teaching mistakes.
Caution: Beware of using behavior charts.
Teachers might be tempted to use behavior charts, behavior bucks, reward and incentive charts, and similar tools thinking that they help improve behaviors, and increase motivation and student productivity. There are web sites that provide such tools, including free printables. However, consider these two questions, posed by Ashley Patek (2019): "Are these systems helping children learn? And are they having long-term positive effects, not only on children's behaviors, but on their sense of self and their mindset?" (Generational Uses section). Such tools can be just extrinsic motivators depending on how teachers use the information collected from such charts. They also have the potential to prevent students from experiencing intrinsic motivation. "Behavioral management charts can have the undesirable side-effect of shaming children into compliance and at the same time, failing to motivate the very children they are often intended to motivate, namely strong-willed children and/or kids that lack the social-emotional skills necessary to meet the desired behavior being monitored by the chart" (Alternatives section).
To help build your confidence in teaching, understanding student behavior, and classroom management, consider the following resources:
 Assertive Discipline: Positive Behavior Management for Today's Classroom
(4th ed.) by Lee Canter (2010). This award-winning book
"outlines a three-step approach for positive behavior management by
creating a classroom discipline plan that includes: rules that
students must follow at all times; positive support that students
will receive consistently for following the rules; and corrective
actions that the teacher will use consistently when students choose
not to follow the rules" (Description section).
Assertive Discipline: Positive Behavior Management for Today's Classroom
(4th ed.) by Lee Canter (2010). This award-winning book
"outlines a three-step approach for positive behavior management by
creating a classroom discipline plan that includes: rules that
students must follow at all times; positive support that students
will receive consistently for following the rules; and corrective
actions that the teacher will use consistently when students choose
not to follow the rules" (Description section).
Avoiding Common Classroom Management Missteps by Michele Hope (2021, December 17). Hope focuses on four missteps and alternative teacher behaviors on avoiding those. Missteps include focusing on rules and procedures rather than on establishing collaborative norms (i.e., an agreement among all members on how they will treat each other), focusing on praise and rewards rather than positive reinforcement of desired behaviors, focusing on punishment rather than correction by encouraging reflection and change, and assuming all students are the same rather than being deliberate about building relationships.
Classroom Management: Teachers Modules by Tom Kratochwill is hosted by the American Psychological Association. Following an introduction, you'll find dos and don'ts, why classroom management works, for whom it works, FAQs, developmental differences, and additional resources.
 THE Classroom Management Book
by Harry Wong and Rosemary Wong (2014) offers 50 procedures that can be used as is or
adapted to fit in any classroom management plan at any grade level.
The authors define classroom management and how it differs from
discipline. You'll find procedures for before and on the first
day of school, procedures for students and teachers, procedures for
the classroom, for instruction (e.g., discussion, group work,
note-taking, reading a text, test taking, for students correcting
work, cultivating social skills), for the special needs classroom, and more.
THE Classroom Management Book
by Harry Wong and Rosemary Wong (2014) offers 50 procedures that can be used as is or
adapted to fit in any classroom management plan at any grade level.
The authors define classroom management and how it differs from
discipline. You'll find procedures for before and on the first
day of school, procedures for students and teachers, procedures for
the classroom, for instruction (e.g., discussion, group work,
note-taking, reading a text, test taking, for students correcting
work, cultivating social skills), for the special needs classroom, and more.
Clever is classroom management program "with resources to help teachers set up and maintain their classrooms for successful digital learning," per its website. Tools include teacher pages to set up your digital classroom, messaging, analytics, and more.
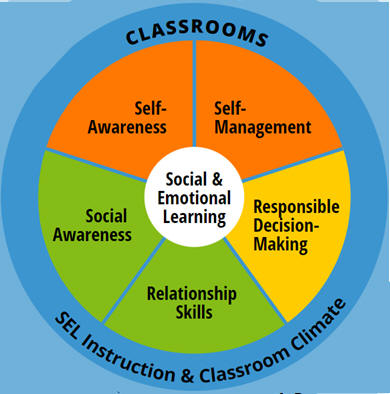 HOT!: Collaborative for Academic, Social, and Emotional Learning
(CASEL) features information on this topic and programs based on social and
emotional learning: What is SEL?, SEL in action, SEL in policy, SEL
research. In
What Does the Research Say? you'll learn about the many benefits of SEL.
See CASEL's list of
SEL
Publications. Math educators might be interested in
Examples of
Social and Emotional Learning in Elementary Mathematics Instruction
(2017, August 20) CASEL also offers a short course on
An
introduction to Social and Emotional Learning, which can be completed at
your own pace in about an hour. It's meant for K-12 educators,
parents, and others interested in SEL.
HOT!: Collaborative for Academic, Social, and Emotional Learning
(CASEL) features information on this topic and programs based on social and
emotional learning: What is SEL?, SEL in action, SEL in policy, SEL
research. In
What Does the Research Say? you'll learn about the many benefits of SEL.
See CASEL's list of
SEL
Publications. Math educators might be interested in
Examples of
Social and Emotional Learning in Elementary Mathematics Instruction
(2017, August 20) CASEL also offers a short course on
An
introduction to Social and Emotional Learning, which can be completed at
your own pace in about an hour. It's meant for K-12 educators,
parents, and others interested in SEL.
How de-escalation strategies can reduce disruptive classroom behaviors by Kara Arundel (2022, January 19) at K-12 Dive is a quick and informative read that delves into seven stages in a classroom behavior crisis cycle and strategies for responding to each. The stages include calm, triggers, agitation, acceleration, peak, de-escalation, and recovery. More details are found in Understanding and Managing the Acting Out Cycle.
IRIS Center at Vanderbilt University includes a series of Evidence-Based Practice Summaries on instructional strategies and interventions, including behavior and classroom management.
The National Education Association has a series of articles on classroom management.
 simSchool
is a simulation program for educators. You can experience the potential of digital games-based
learning as you practice your teaching skills. You'll get immediate feedback on how your selected strategies
affect student learning. Plus, as in a real classroom, the simStudents
will react to user-selected task design, as well as your teacher moves.
simSchool
is a simulation program for educators. You can experience the potential of digital games-based
learning as you practice your teaching skills. You'll get immediate feedback on how your selected strategies
affect student learning. Plus, as in a real classroom, the simStudents
will react to user-selected task design, as well as your teacher moves.
The Teacher's Guide has a wealth of information on classroom management with strategies, lessons, videos, discussion groups, books, and printouts.
25 Time-Saving Grading Apps To Make Teachers Lives Easier
 "Teacher resource apps are designed to assist teachers in
completing common tasks (e.g., taking attendance, communicating with
parents, monitoring student learning and behavior, etc.)" (Cherner,
Lee, Fegely, Santaniello, 2016, p. 117). The market is flooded
with such apps that teachers can use to manage their classrooms and
tasks. Quality varies, however, and selecting one based on a
star-rating system might not be sufficient.
"Teacher resource apps are designed to assist teachers in
completing common tasks (e.g., taking attendance, communicating with
parents, monitoring student learning and behavior, etc.)" (Cherner,
Lee, Fegely, Santaniello, 2016, p. 117). The market is flooded
with such apps that teachers can use to manage their classrooms and
tasks. Quality varies, however, and selecting one based on a
star-rating system might not be sufficient.
Sometimes, its also best to weigh the cost of an app versus its effectiveness, particularly if a resource is intended for student learning. Try to consult others who use it and look for research conducted on any considerations. For example, Finster, Decker- Woodrow, Booker, Mason, Tu, and Lee (2023) presented their "cost-effective analysis (CEA) of three algebraic technological applications, across four conditions: From Here to There (FH2T), Dragon Box 12+ (DragonBox), Immediate Feedback and Active Control." Overall, the study demonstrated "the efficiency of FH2T and DragonBox as low-cost interventions for improving students’ algebraic performance and addressing the nation’s decline in mathematics." (Abstract section)
So, how do you select one?
CT4ME has a Math Software and App Evaluation Form to help in selection.
HOT Rubric: Cherner, T., Lee, C-Y., Fegely, A., & Santaniello, L. (2016). A detailed rubric for assessing the quality of teacher resource apps. Journal of Information Technology Education: Innovations in Practice, 15,117-143. https://www.informingscience.org/Publications/3527
Cherner and his colleagues developed their Evaluation Rubric for Teacher Resource Apps (see Appendix A) to help teachers assess strengths and weaknesses of resource apps they might wish to use. As discussed in their 2016 publication, the dimensions fall within three domains: Efficiency, Functionality, and Design.
All teachers must include goals to become familiar with teacher standards, subject matter standards and benchmark indicators at the state and national levels. CT4ME provides this information in our section on Standards. Common Core Math Standards are at the forefront, as many states have adopted them. These frameworks specify standards that students should achieve, but do not specify the curriculum and teaching methods to be used. For this, teachers need to examine the district curriculum for how their schools and teachers aligned standards with content to be taught. They need to examine scope and sequence, instructional materials, implementation strategies, and any suggested pedagogical methods.
| Domains within the Common Core Math Standards | |||||||||
| K | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | HS |
| Counting & Cardinality | |||||||||
| Number & Base 10 Operations |
Ratios & Proportions | Number & Quantity | |||||||
| Number Operations Fractions | Number System | Algebra | |||||||
| Operations & Algebraic Thinking |
Expressions & Equations | Algebra | |||||||
| Operations & Algebraic Thinking |
Functions | Functions | |||||||
| Geometry | Geometry | ||||||||
| Measurement & Data | Statistics & Probability | Statistics & Probability | |||||||
| Source: Common Core State Standards (2010). Mathematics Standards. Washington, DC: National Governors Association Center for Best Practices, Council of Chief State School Officers. https://www.thecorestandards.org/Math/ | |||||||||
The Common Core State Standards (CCSS) for Mathematics (2010) include eight standards for mathematical practice that "describe varieties of expertise that mathematics educators at all levels should seek to develop in their students." They include:
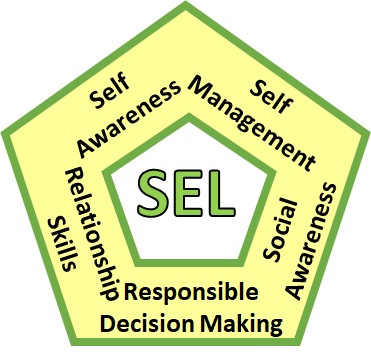 As
educators examine the Common Core Standards for Mathematical Practice,
it becomes clear that the standards "reflect the view that learning is a
social process, implicitly calling for teaching practices that leverage the
power of group work and collaborative learning" (Charles A. Dana Center at The University of Texas at
Austin and the Collaborative for Academic, Social, and Emotional Learning
(CASEL), 2016, p. 1). The mathematical practice standards embed five core
social-emotional learning (SEL) competencies, which CASEL identified as "self-awareness, self-management,
social awareness, relationship skills, and responsible decision making" (p. 2).
Consider the first standard of mathematical practice (SMP 1). To illustrate its
SEL connection, the Dana Center and CASEL stated:
As
educators examine the Common Core Standards for Mathematical Practice,
it becomes clear that the standards "reflect the view that learning is a
social process, implicitly calling for teaching practices that leverage the
power of group work and collaborative learning" (Charles A. Dana Center at The University of Texas at
Austin and the Collaborative for Academic, Social, and Emotional Learning
(CASEL), 2016, p. 1). The mathematical practice standards embed five core
social-emotional learning (SEL) competencies, which CASEL identified as "self-awareness, self-management,
social awareness, relationship skills, and responsible decision making" (p. 2).
Consider the first standard of mathematical practice (SMP 1). To illustrate its
SEL connection, the Dana Center and CASEL stated:
"SMP 1 students “Make sense of problems and persevere in solving them.” Mathematically proficient students “...understand the approaches of others to solving complex problems and identify correspondences between different approaches.” To effectively engage in this practice, students must be able to stay calm when facing a challenging problem (self-management), recognize when they lack the knowledge to solve a problem (self-awareness), effectively solicit help from others (relationship skills), and learn from others how they solve problems (social awareness)." (p. 3)
The Dana Center and CASEL (2016) elaborated on the SEL connections to each of the mathematical practice standards. Think of those SEL competencies as you examine the following on How to Help Students Meet the Common Core Standards for Mathematics. The eight mathematical practices are circled.
Learn more about mathematics instruction for perseverance and SEL with the following resources:
Keep Going! Building a Culture of Perseverance in Math Classrooms from PBS LearningMedia "is a collection of classroom video examples and background materials to help high school teachers understand and implement the Problem Solving and Perseverance standard from the Common Core Standards for Mathematical Practice."
Academic Social and Emotional Learning (SEL) and Mathematics Curriculum Materials is a SEL tool from the Charles A. Dana Center at the University of Texas at Austin. Use it "to determine if your mathematics instructional materials support students’ understanding and application of widely accepted social and emotional learning (SEL) competencies." Further, students "also need direct instruction in each of the SEL competencies, and teachers need specific training in the SEL competencies and how to incorporate them into daily instructional practice" per the tool's description.
Also consider the following book:
 All Learning is Social and Emotional: Helping Students Develop Essential Skills
for the Classroom and Beyond by Nancy Frey, Douglas Fisher, and Dominique
Smith (2019). The authors provide a five-part model of SEL applicable at
any grade level and in any subject. Per its description, "Along with a
toolbox of strategies for addressing 33 essential competencies, you'll find
real-life examples highlighting the many opportunities for social and emotional
learning within the K–12 academic curriculum."
All Learning is Social and Emotional: Helping Students Develop Essential Skills
for the Classroom and Beyond by Nancy Frey, Douglas Fisher, and Dominique
Smith (2019). The authors provide a five-part model of SEL applicable at
any grade level and in any subject. Per its description, "Along with a
toolbox of strategies for addressing 33 essential competencies, you'll find
real-life examples highlighting the many opportunities for social and emotional
learning within the K–12 academic curriculum."
Linda Gojak (2012), former President of the National Council of Teachers of Mathematics (NCTM), noted that "Over the last three decades a variety of instructional strategies have been introduced with a goal of increasing student achievement in mathematics. Such strategies include individualized instruction, cooperative learning, direct instruction, inquiry, scaffolding, computer-assisted instruction, and problem solving" (para. 1). The flipped classroom is a recent addition to the list. Blended learning is also on the rise, which adds online learning to traditional classrooms. The recent attention to the use of math tools that incorporate generative artificial intelligence has added a new dimension to teaching mathematics. Thus, another goal for teachers is to investigate instructional and assessment methods and how they might be incorporated appropriately into classrooms.
In a standards-based classroom four instructional strategies are key:
In its Principles to Actions: Ensuring Mathematical Success for All, NCTM (2014) indicated the following research-based mathematics teaching practices, which should be "consistent components of every mathematics lesson":
NCTM released its position on Artificial Intelligence and Mathematics Teaching (2024, February). Its position on the use of AI refers to "technologies derived from generative AI machine learning approaches (e.g., ChatGPT, Bard, etc.)" (Defining Terms section). Key takeaways: Although generative AI has the potential to personalize learning and streamline teaching tasks, "AI tools do not replace the need to teach math or problem solving." AI output might include biased data, hallucinations (untrue or unreaonable results), and inaccurate citations, making it important for educators to tell students to be skeptical of results and to teach them how to verify results, which they also must learn how to do. NCTM's position notes that "AI tools encourage teachers to reimagine teaching and assessment. Blending the fundamental computational skills with sensemaking and creative problem solving requires a deep understanding of the math involved, as well as a deep understanding of Pedagogical Content Knowledge (PCK) and Mathematical Knowledge for Teaching (MKT). Educators lacking this expertise can fall into the trap of repetitive, strictly computation 'shallow assessments.' " Further, to add another dimension to teaching, math educators will "need to be involved in developing and testing AI tools in math education to stay up to date with current AI trends to best prepare students for an AI future." All this requires "math teachers with more experience, not less."
All teachers should consider the role of active or constructivist learning, as opposed to using only a lecture method. The teacher becomes a facilitator in a student-centered approach. The 5E instructional model (Engagement, Exploration, Explanation, Elaboration, Evaluation) has been considered one of the most effective teaching models within a constructivist learning approach, as noted by Stephen Akinyemi Omotayo and Joshua Oluwatoyin Adeleke (2017). They described each phase in the model in their research, The 5E Instructional Model: A constructivist approach for enhancing students' learning outcomes in mathematics.
Active student involvement reinforces learning. This is not to minimize the role of direct instruction, however. Madeline Hunter's teacher-centered, direct instructional model has influenced lesson planning since the 1980s. The model, called Instructional Theory into Practice (ITIP), includes eight elements: an anticipatory set, objective and purpose, input, modeling, checking for understanding, guided practice, independent practice, and closure (Cuban, 2019). California State University Northridge has posted The Madeline Hunter Model of Mastery Learning.
 Students should become active in the learning process immediately
upon entering the classroom. Muschla, Muschla, and Muschla-Berry
(2013) stated: "Classes in which students begin working from the minute
they take their seats are usually more successful than those in which
the first few minutes are lost as the students get settled" (p. 3).
Losing just the first five minutes daily amounts to 25 lost minutes per
week of instruction and could amount to a loss of 20 class periods of
instruction per school year. Their solution is using a
math-starter problem that students begin immediately upon entering the classroom. In
Math Starters: 5- to 10-Minute Activities Aligned with the Common Core Math Standards, Grades 6-12,
they present at least one problem for each Common Core math standard for grades
6-12. Each is designed to be completed in 5-10 minutes, which includes
reviewing the answer and any follow-up discussion. This strategy is also
good for classroom management, as during this time the teacher can take
attendance, pass back papers, interact individually with students, and observe
students as they work (p. 3).
Students should become active in the learning process immediately
upon entering the classroom. Muschla, Muschla, and Muschla-Berry
(2013) stated: "Classes in which students begin working from the minute
they take their seats are usually more successful than those in which
the first few minutes are lost as the students get settled" (p. 3).
Losing just the first five minutes daily amounts to 25 lost minutes per
week of instruction and could amount to a loss of 20 class periods of
instruction per school year. Their solution is using a
math-starter problem that students begin immediately upon entering the classroom. In
Math Starters: 5- to 10-Minute Activities Aligned with the Common Core Math Standards, Grades 6-12,
they present at least one problem for each Common Core math standard for grades
6-12. Each is designed to be completed in 5-10 minutes, which includes
reviewing the answer and any follow-up discussion. This strategy is also
good for classroom management, as during this time the teacher can take
attendance, pass back papers, interact individually with students, and observe
students as they work (p. 3).
John Malouff (2018) grouped and explained over 50 problem-solving strategies, many of which can be applied to mathematics problem solving. Strategies can help understand the problem, simplify the task, determine the cause of a problem, involve external aids to help identify problem solutions, use logic to help identify possible solutions. Strategies can also identify a possible solution to serve as a starting point to solve a problem, or determine which possible solution is best. Strategies can employ geometric thinking, help you to function optimally while problem solving, and help solve multiple problems. George Polya's Problem-Solving Techniques contain details of his four principles that have become a classic for math problem-solving: understand the problem, devise a plan, carry out the plan, and look back.
The IRIS Center at Vanderbilt University provides details on evidence-based strategies for teaching mathematics in its module: High-Quality Mathematics Instruction: What Teachers Should Know (2017). An initial step is to adopt a standards-based curriculum, after which evidence-based programs and practices can be selected. The IRIS module addresses the following strategies, which have moderate to strong evidence for improving outcomes for students in mathemtics: explicit, systematic instruction; visual representations, schema instruction, and metacognitive strategies (e.g., self-instruction and self-monitoring).
Cautions: According to Robert Coe, Cesare Aloisi, Steve Higgins, and Lee Elliot Major (2014), teachers have been known to use instructional strategies that have not been supported by research. Examples of such ineffective practices include using praise lavishly, allowing students to discover key ideas for themselves (i.e., a caution about discovery learning), grouping learners by ability, encouraging re-reading and highlighting to memorize key ideas, addressing issues of confidence and low aspirations before you try to teach content, presenting information to learners in their preferred learning style, and ensuring learners are always active, rather than listening passively, if you want them to remember (pp. 22-24). They concluded "...if you want students to remember something you have to get them to think about it. This might be achieved by being ‘active’ or ‘passive’ " (p. 24).
Assessing student understanding and designing instruction to meet learners' needs are challenging tasks. Popham (2009) noted that assessment is a broad term:
Assessment includes both traditional paper-and-pencil exams, such as those made up of True/False, short-answer, or multiple-choice items, and a much larger collection of procedures that teachers can use to get a fix on their students' status, including the use of portfolios to document students' evolving skills and the use of anonymous self-report inventories to measure students' attitudes or interests. Assessments also include the variety of informal techniques a teacher might use to check on the status of students' skills for the purpose of guiding instruction rather than for grade-giving, such as when a teacher periodically projects multiple-choice questions on a screen during a lesson and asks students, "on the count of three," to hold up one of four prepared index cards showing the letter of what each student believes is the correct answer. (Popham, 2009, Preface section, para. 6)
Thus, formative assessment plays a major role, and its importance should not be overlooked in our zeal to prepare students for mandated accountability tests. See Part 2 of this essay for more on the role of assessment.
Test preparation is a reality. CT4ME has an entire section devoted to standardized test preparation.
The Center for Research on Learning and Teaching at the University of Michigan provides Inclusive Teaching Strategies and an Introduction to Active Learning with related resources for its implementation.
The Effective Mathematics Classroom from the Leadership Department of Andrews University
HOT! The Mathematics Hub: Teaching Strategies section elaborates on teaching strategies aligned to six principles for effective teaching of mathematics. The six principles are articulating goals, making connections, fostering engagement, differentiating challenges, structuring lessons, and promoting fluency and transfer. For more on these principles, read Teaching Mathematics: Using research-informed strategies by Peter Sullivan (2011).
The Science of Math provides resources on effective math instruction. The site indicates it relies on "well-researched instructional strategies and research about how students learn." It also includes a section addressing math misconceptions.
The following also provide evidence-based strategies:
Also consider the following books and articles:
 The Inclusive Classroom: Strategies for
Effective Differentiated Instruction, 6th ed., by Margo Mastropieri
and Thomas Scruggs (2018). Per its description, this book contains
research-based classroom and content strategies. The authors "explain
the fundamentals of inclusive teaching, the most effective general teaching
practices, and ways to differentiate instruction for specific content
areas." Learn "ways to improve all students' memory, attention,
motivation, study skills, and peer interaction." You'll find content
on response to intervention, multi-tiered systems fo support, Universal
Design for Learning, the latest strategies for academic success, and
coverage of the Common Core standards. An entire chapter is devoted to
mathematics. Chapters also include strategies for teaching learners
with special needs.
The Inclusive Classroom: Strategies for
Effective Differentiated Instruction, 6th ed., by Margo Mastropieri
and Thomas Scruggs (2018). Per its description, this book contains
research-based classroom and content strategies. The authors "explain
the fundamentals of inclusive teaching, the most effective general teaching
practices, and ways to differentiate instruction for specific content
areas." Learn "ways to improve all students' memory, attention,
motivation, study skills, and peer interaction." You'll find content
on response to intervention, multi-tiered systems fo support, Universal
Design for Learning, the latest strategies for academic success, and
coverage of the Common Core standards. An entire chapter is devoted to
mathematics. Chapters also include strategies for teaching learners
with special needs.
Protheroe, N. (2007). What does good math instruction look like? Principal, 7(1), 51-54. https://www.naesp.org/resources/2/Principal/2007/S-Op51.pdf
Shing, C. L., Saat, R. M., & Siow H. (2015). The knowledge of teaching--Pedagogical content knowledge (PCK). Malaysian Online Journal of Educational Sciences, 3(3), 40-55. https://files.eric.ed.gov/fulltext/EJ1085915.pdf
The following delves into theory and research; learning styles, multiple intelligences and thinking styles; and differentiated instruction and the educator's ideology.
 Every
teacher should have some knowledge on how people learn and be able to
connect research to what they do in the classroom. For example, how people
learn is influenced by culture, including observations and interactions with
individuals and experts, the culture of the school and classroom, and that of
the individual student. Context plays a role, as do social interactions,
physical exercise, sleep, nutrition, mental models, and motivation (National
Academies of Sciences, Engineering, and Medicine, 2018).
Every
teacher should have some knowledge on how people learn and be able to
connect research to what they do in the classroom. For example, how people
learn is influenced by culture, including observations and interactions with
individuals and experts, the culture of the school and classroom, and that of
the individual student. Context plays a role, as do social interactions,
physical exercise, sleep, nutrition, mental models, and motivation (National
Academies of Sciences, Engineering, and Medicine, 2018).
The American Psychological Association, Coalition for Psychology in Schools and Education (2015) identified eight principles on how students think and learn:
How do you foster creativity in math? Pronita Mehrotra (2019) suggested Five Simple Ways to Add Creativity in Mathematics:
In The Science of Learning, the Deans for Impact (2015) provided a valuable summary of cognitive science research on how learning takes place. In it you'll find cognitive principles and numerous practical implications for the classroom related to six key questions on how students understand new ideas, learn and retain new information, and solve problems; how learning transfers to new situations; what motivates students to learn; and common misconceptions about how students think and learn. The following are among those principles and classroom implications:
Likewise, the Centre for Education Statistics and Evaluation (2017) in New South Wales, Australia elaborated on research that teachers really need to understand about cognitive load theory: what it is, how the human brain learns, the evidence base for the theory, and implications for teaching. For example, when teaching, you'll learn about the effect of using worked examples with novices and learners who gain expertise, the effect of redundancy (unnecessary information might actually lead to instructional failure), the negative effect of split-attention (processing multiple separate sources of information simultaneously in order to understand the material), and the benefit of using supporting visual and auditory modalities.
In their review of over 200 studies in What makes great teaching?, Robert Coe, Cesare Aloisi, Steve Higgins, and Lee Elliot Major (2014) identified elements of teaching with the strongest evidence of improving student achievement. In order of strength, those factors included:
Their review also delved into some common "practices whose use is not supported by research evidence" (p. 22):
In Improving Mathematics Teaching, James Stigler and James Hiebert (2004) indicated that teachers need theories, empirical research, and alternative images of what implementation of problem solving strategies looks like. U.S. teachers need assistance with making connections problems. As they might never have seen what it looks like to implement such problems effectively, they tend to turn making connections problems into procedural exercises.
There is much to be learned about improving instruction by examining initiatives within the U.S. that provide educators with the best-practice examples they might need. Inside Mathematics, which grew out of the Noyce Foundation's Silicon Valley Mathematics Initiative, is exemplary as a professional resource for educators passionate about improving students' mathematics learning and performance. This site features tools for educators, problems of the month, classroom videos, Common Core resources, and performance assessment tasks.
Teachers can also improve instruction by examining what takes place in other countries. For example, the Trends in International Mathematics and Science (TIMSS) 1999 video study examined an alternative methodology that holds promise to improve math instruction in the U.S. Details and videos are available at http://www.timssvideo.com. You'll find multiple math video lessons from several countries, including Australia, Netherlands, the Czech Republic, Japan, Hong Kong, Switzerland, and the U.S. with translations into English.
Japanese Lesson Study is growing in the U.S. as a result of the TIMSS study. "This planning and lesson analysis protocol typically consists of three sequential activities. First, teachers collaborate in the planning of a lesson, pursuing a common goal of learning that they hope their students will achieve. Next, a small group teaches the resulting lesson while other teachers perform action research on the lesson as it is taught. Finally, researchers and observers disclose their findings in a follow-up session, identifying the lesson's successful elements" (O'Shea, 2005, pp. 24-25). This collaborative process enables teachers to develop more effective lessons.
For more on the work of TIMSS, see the following:
Effective lessons incorporate best-practice. According to Daniels and Bizar (1998, as cited in Wilcox & Wojnar, 2000), there are six methods that matter in a " best practice classroom." These are integrative units, small group activities, representing to learn through multiple ways of investigating, remembering, and applying information; a classroom workshop teacher-apprentice approach, authentic experiences, and reflective assessment. Further, Mike Schmoker (2006) stated that "the most well-established elements of good instruction [include]: being clear and explicit about what is to be learned and assessed; using assessments to evaluate a lesson's effectiveness and making constructive adjustments on the basis of results; conducting a check for understanding at certain points in a lesson; having kids read for higher-order purposes and write regularly; and clearly explicating and carefully teaching the criteria by which student work will be scored or evaluated" (p. 25). In mathematics classrooms, teachers might tend to ignore writing about the discipline; however, to develop complex knowledge, "students need opportunities to read, reason, investigate, speak, and write about the overarching concepts within that discipline" (McConachie et al., 2006, p. 8).
Also consider the following books:
 Results
Now 2.0: the Untapped Opportunities for Swift, Dramatic Gains in Achivement
by Mike Schmoker (2023). This book expands on Schmoker's 2006 edition
of Results Now. He addresses the gap between instructional
best practices and what is taught (and not taught) in classrooms today
(i.e., the gap between proven practice and common practice). He
advocates a focus on the fundamental elements of curriculum, literacy, and
effective instruction to improve the K-12 education system and provides
examples of schools that have successfully used evidence and strategic
practice.
Results
Now 2.0: the Untapped Opportunities for Swift, Dramatic Gains in Achivement
by Mike Schmoker (2023). This book expands on Schmoker's 2006 edition
of Results Now. He addresses the gap between instructional
best practices and what is taught (and not taught) in classrooms today
(i.e., the gap between proven practice and common practice). He
advocates a focus on the fundamental elements of curriculum, literacy, and
effective instruction to improve the K-12 education system and provides
examples of schools that have successfully used evidence and strategic
practice.
 The Science of Learning: 99 Studies
that Every Teacher Needs to Know, 2nd edition, by Edward Watson and
Bradley Busch (2021). The authors delve into studies within seven topics: memory;
mindset, motivation and resilience; self-regulation and metacognition;
student behaviors; teacher attitudes, expectations, and behaviors; parents;
and thinking biases. Each study includes main findings, related
research, and implications for classroom practice. For example, this
2nd edition includes 22 new studies on cognitive load theory, well-being,
and performing well under exam pressure.
The Science of Learning: 99 Studies
that Every Teacher Needs to Know, 2nd edition, by Edward Watson and
Bradley Busch (2021). The authors delve into studies within seven topics: memory;
mindset, motivation and resilience; self-regulation and metacognition;
student behaviors; teacher attitudes, expectations, and behaviors; parents;
and thinking biases. Each study includes main findings, related
research, and implications for classroom practice. For example, this
2nd edition includes 22 new studies on cognitive load theory, well-being,
and performing well under exam pressure.
 The New Art and Science of Teaching
Mathematics (Establish Effective Teaching Strategies in Mathematics
Instruction) Illustrated Edition by Nathan Lang-Raad and Robert Marzano
(2019). This book will help educators to implement research-based best
practices in teaching mathematics. The authors present a framework
with 10 design areas and 43 elements of effective teaching strategies and in
which lessons they should be used.
The New Art and Science of Teaching
Mathematics (Establish Effective Teaching Strategies in Mathematics
Instruction) Illustrated Edition by Nathan Lang-Raad and Robert Marzano
(2019). This book will help educators to implement research-based best
practices in teaching mathematics. The authors present a framework
with 10 design areas and 43 elements of effective teaching strategies and in
which lessons they should be used.
 Small changes in math instruction can help students to make sense of
mathematics and empower them as mathematicians. In her work with
novice teachers, Corey Drake (2016) emphasizes the following strategies, which
are easily managed within the classroom, and meaningful to students:
Small changes in math instruction can help students to make sense of
mathematics and empower them as mathematicians. In her work with
novice teachers, Corey Drake (2016) emphasizes the following strategies, which
are easily managed within the classroom, and meaningful to students:
The Teaching Channel has a series called the New Teacher Survival Guide. Within it are essential questions with related resources and videos on planning, classroom management, differeniating instruction, mentoring, and more.
 Many students experience math anxiety.
Much of this stems from a one style fits all approach to teaching.
Traditionally, approaches to teaching mathematics have focused on linguistic and
logical teaching methods, with a limited range of teaching strategies.
Some students learn best, however, when surrounded by movement and sound, others
need to work with their peers, some need demonstrations and applications that
show connections of mathematics to other areas (e.g., music, sports,
architecture, art), and others prefer to work alone, silently, while reading
from a text. All of this is reflected in
Howard
Gardner's Theory of Multiple Intelligences, which has found its way into
schools (Moran, Kornhaber, & Gardner, 2006; Smith, 2002, 2008), along with the
concept of learning styles.
Many students experience math anxiety.
Much of this stems from a one style fits all approach to teaching.
Traditionally, approaches to teaching mathematics have focused on linguistic and
logical teaching methods, with a limited range of teaching strategies.
Some students learn best, however, when surrounded by movement and sound, others
need to work with their peers, some need demonstrations and applications that
show connections of mathematics to other areas (e.g., music, sports,
architecture, art), and others prefer to work alone, silently, while reading
from a text. All of this is reflected in
Howard
Gardner's Theory of Multiple Intelligences, which has found its way into
schools (Moran, Kornhaber, & Gardner, 2006; Smith, 2002, 2008), along with the
concept of learning styles.
Moran et al. (2006) indicated that multiple intelligences theory proposes viewing intelligence in terms of nine cognitive capacities, rather than a single general intelligence. Thus, a profile consists of strengths and weaknesses among "linguistic, logical-mathematical, musical, spatial, bodily-kinesthetic, naturalistic, interpersonal, intrapersonal, and (at least provisionally) existential" (p. 23). Overall, the theory has been misunderstood in application.
The multiple intelligences approach does not require a teacher to design a lesson in nine different ways to that all students can access the material...In ideal multiple intelligences instruction, rich experiences and collaboration provide a context for students to become aware of their own intelligence profiles, to develop self-regulation, and to participate more actively in their own learning. (p. 27)
Multiple intelligences (MI) and learning styles (LS) are not interchangeable terms. According to Barbara Prashnig (2005), "LS can be defined as the way human beings prefer to concentrate on, store, and remember new and/or difficult information. MI is a theoretical framework for defining/ understanding/ assessing/ developing people's different intelligence factors" (p. 8). Consider LS as "explaining information 'INPUT' capabilities" and MI "more at the 'OUTPUT' function of information intake, knowledge, skills, and 'talent'--mathematical, musical, linguistic" and so on (p. 9).
Indeed, Howard Gardner has stated that multiple intelligences are not learning styles. In Gardner's view, a style or learning style "is a hypothesis of how an individual approaches the range of materials." There are two basic problems. First, "the notion of 'learning styles' is itself not coherent. Those who use this term do not define the criteria for a style, nor where styles come from, how they are recognized/ assessed/ exploited." Second, "When researchers have tried to identify learning styles, teach consistently with those styles, and examine outcomes, there is not persuasive evidence that the learning style analysis produces more effective outcomes than a 'one size fits all approach.' " Labeling a style (e.g., visual or auditory learner) might actually be unhelpful or inconceived. Putting a label on it does not mean the "style" fits all learning scenarios (Gardner, in Strauss, 2013).
Knowledge of how students learn best assists teachers in developing lessons that appeal to all learners. However, determining a student's learning "style" cannot be done strictly by observation. Various models and inventories have been designed to determine a learning style. Labeling a "style" poses an additional problem in that a style does not remain fixed over time. Therein lies the main concern of relying on inventories, as their validity and reliability might be in question (Dembo & Howard, 2007), and they differ. The following are among those inventories:
The Dunn and Dunn Model includes "environmental, emotional, sociological, physiological, and psychological preferences" per its description at Learning Abled Kids.
David Kolb's Learning Styles Inventory categorizes in four dimensions (converger, diverger, assimilator, or accommodator) based on the degrees to which one possesses "concrete experience abilities, reflective observation abilities, abstract conceptualization abilities and active experimentation abilities" (Smith, 2001, David Kolb on Learning Styles section). Note: David Kolb's website: Experienced Based Learning Systems, Inc includes his inventory and more information on learning styles.
VARK (Visual, Aural, Read/write, and Kinesthetic) is only part of a learning style, according to developer Neil Fleming who states "VARK is about one preference -our preference for taking in, and putting out information in a learning context"; "VARK is structured specifically to improve learning and teaching." The VARK questionnaire (just 16 short questions) is available online.
The Index of Learning Styles is a 44-question on-line instrument with automatic scoring on the Web that was developed by Richard Felder and Barbara Soloman of North Carolina State University. This model assesses learning preferences on four dimensions (active/reflective, sensing/intuitive, visual/verbal, and sequential/global).
As an alternative to determining learning styles, a personal Thinking Styles Inventory and The Multiple Intelligence Inventory based on Gardner's work will also benefit teaching and learning. Students with learning disabilities or attention-deficit-disorder can find practical tips on how to make your learning style work for you at LdPride.net, which also contains more information on multiple intelligences.
With so many inventories available, teachers might wonder how their teaching can accommodate so many styles. Li-fang Zhang and Robert Sternberg (2005) indicated, however, that teachers need only to attend to "five basic dimensions of preferences underlying intellectual styles: high degrees of structure versus low degrees of structure, cognitive simplicity versus cognitive complexity, conformity versus nonconformity, authority versus autonomy, and group versus individual. Furthermore, [they] believe that good teaching treats the two polar terms of each dimension as the two ends of a continuum and provides a balanced amount of challenge and support along each dimension" (p. 43).
Readers should be aware that there is no scientific support of the idea that learning styles impact learning outcomes. Yet many educators hold that belief, a conclusion that Ulrich Boser (2019) found from his survey research on What do teachers know about the science of learning? His survey revealed that 97% of respondents endorsed the idea of learning styles and that these impact how people learn. His research also revealed that 77% of educators believed that there are "left-brained" and "right-brained" learners and that this difference also affects how they learn, yet this is also a myth as there is no scientific evidence to support it. Boser (2019) is among many who have addressed the myth of learning styles.
According to Dembo and Howard (2007), "The bottom line is that there is no consistent evidence that matching instruction to students' learning styles improves concentration, memory, self-confidence, grades, or reduces anxiety" (p. 106). Rather, Dembo and Howard indicated, "The best practices approach to instruction can help students become more successful learners" (p. 107). Such instruction incorporates "Educational research [that] supports the teaching of learning strategies...; systematically designed instruction that contains scaffolding features...; and tailoring instruction for different levels of prior knowledge" (p. 107).
Cognitive scientists Pashler, McDaniel, Rohrer, and Bjork (2009) supported this position and stated, "Although the literature on learning styles is enormous, very few studies have even used an experimental methodology capable of testing the validity of learning styles applied to education. Moreover, of those that did use an appropriate method, several found results that flatly contradict the popular meshing hypothesis" (p. 105). They concluded "at present, there is no adequate evidence base to justify incorporating learning-styles assessments into general educational practice" (p. 105) and "widespread use of learning-style measures in educational settings is unwise and a wasteful use of limited resources. ... If classification of students' learning styles has practical utility, it remains to be demonstrated" (p. 117).
Willingham, Hughes, and Dobolyi (2015) confirmed that we have a responsibility to ensure that students know that learning styles theories have not panned out (p. 269). Further, Willingham (2018) concluded, "Although there’s scant evidence that matching the manner of processing to a student’s preferred style brings any benefit, there’s ample evidence that matching the manner of processing to the task helps a lot. Students can be taught useful strategies for committing things to memory, reading with comprehension, overcoming math anxiety, or avoiding distraction, for example. Learning styles do not influence the effectiveness of these strategies" (p. 32).
Philip Newton and Atharva Salvi (2020) conducted a review of research on beliefs and use of learning styles that involved 37 studies from 2009 to early 2020 representing over 15,000 educators in18 countries. Their summary conclusion indicated "a substantial majority of educators, almost 90%, from samples all over the world in all types of education, report that they believe in the efficacy of a teaching technique that is demonstrably not effective and potentially harmful. There is no sign that this is declining, despite many years of work, in the academic literature and popular press, highlighting this lack of evidence." As found in their introductory review of literature, the proposed harms include such things as:
Ultimately, although we might continue to argue over terminology and labels associated with learning, Gardner (in Strauss, 2013) provided the following lessons for educators:
- Individualize your teaching as much as possible. Instead of “one size fits all,” learn as much as you can about each student, and teach each person in ways that they find comfortable and learn effectively. Of course this is easier to accomplish with smaller classes. But ‘apps’ make it possible to individualize for everyone.
- Pluralize your teaching. Teach important materials in several ways, not just one (e.g. through stories, works of art, diagrams, role play). In this way you can reach students who learn in different ways. Also, by presenting materials in various ways, you convey what it means to understand something well. If you can only teach in one way, your own understanding is likely to be thin.
- Drop the term "styles." It will confuse others and it won't help either you or your students. (Gardner, in Strauss, 2013)
Robert Slavin (2019) said it well:
"What really matters is what teachers do. Give me a teacher who knows how to make content exciting and comprehensible, one who knows how to manage diverse classrooms so that students are eager to learn, self-motivated, productive, and able to work effectively with peers. Give me a teacher who models curiosity, kindness, and flexibility, one who accepts and builds on student errors, one who helps all students believe in themselves and their potential, whatever their backgrounds. If a teacher can do all of these things, do we really care if they think there are learning styles?"
For more on multiple intelligences and learning styles, consult the following:
 Multiple Intelligences in the Classroom, 4th Edition
by Thomas Armstrong (2017)
Multiple Intelligences in the Classroom, 4th Edition
by Thomas Armstrong (2017)
Big Thinkers: Howard Gardner on Multiple Intelligences -- listen to Gardner in this short video posted at Edutopia.org: https://www.edutopia.org/multiple-intelligences-howard-gardner-video
Visit Howard Gardner's website to learn more about him, his theory, and publications: https://www.howardgardner.com. The MI Oasis is his Official Authoritative Site of Multiple IntelligenceS.
Tapping into Multiple Intelligences, a self-paced workshop from Concept to Classroom at Thirteen Ed Online: https://www.thirteen.org/edonline/concept2class/mi/index.html
Walter McKenzie's Surfaquarium: http://surfaquarium.com/MI/ has content devoted to Multiple Intelligences in Education (e.g., an overview of MI, media and software selection, MI and instruction, templates, etc.).
Institute for Learning Styles Research: https://www.learningstyles.biz/
Hale, J. (2019, April 24). The education myth about learning styles. Center for Inquiry Blog. https://centerforinquiry.org/blog/the-education-myth-about-learning-styles/ Jamie Hale supports his commentary with several research studies to debunk the myth on the value of learning styles. He concluded, "There is a large body of research on strategies to maximize learning, and educators and students are advised to review and use information from that line of research instead of spending time trying to identify their illusive learning style."
 Using video and audio to support multiple
intelligences and varied learning preferences and
disabilities is one of the strategies noted by Tomlinson and McTighe's (2006)
to support differentiated instruction. Here's a
sampling of video sites for your consideration in
support of their recommendation:
Using video and audio to support multiple
intelligences and varied learning preferences and
disabilities is one of the strategies noted by Tomlinson and McTighe's (2006)
to support differentiated instruction. Here's a
sampling of video sites for your consideration in
support of their recommendation:
HOT: SchoolTube contains numerous videos on mathematics, which would help learners review concepts presented in class and in some cases offer a different instruction perspective. "SchoolTube provides students and educators a safe, world class, and FREE media sharing website that is nationally endorsed by premier education associations."
HOT: Teacher Tube provides "an online community for sharing instructional videos. ... It is a site to provide anytime, anywhere professional development with teachers teaching teachers. As well, it is a site where teachers can post videos designed for students to view in order to learn a concept or skill."
For additional video resources at this site, see Math Resources: Integrating Podcasts, Vodcasts and Whiteboards into Teaching and Learning at this site.
Teachers have several reasons for using television and video in their instruction, according to results of a 2009 national online survey of 1,418 full time pre-K and K-12 teachers on their use of media and technology. The study, "Digitally Inclined," was conducted by Grunwald Associates for PBS. Teachers believed television and video reinforces and expands on content they are teaching (87%), helps them respond to a variety of learning styles (76%), increases student motivation (74%), changes the pace of classroom instruction (66%), enables them to demonstrate content they can't show any other way (57%), enables them to introduce other learning activities (51%), and helps them teach current events and breaking news (38%). Further, teachers perceived benefits to instruction. They agreed that using television and video stimulates discussion (58%), helps them be more effective (49%) and creative (44%). They agreed that students prefer television and video over other types of instructional resources or content (48%), and it stimulates student creativity (36%). (PBS & Grunwald Associates LLC, 2009, p. 8)
Common Core State Standards (2010) for Mathematical Practice include varieties of expertise that mathematics educators should strive to develop in students at all levels:
Acquiring this expertise will require that educators play greater attention to differentiated instruction. "Differentiated instruction is a process to approach teaching and learning for students of differing abilities in the same class. The intent of differentiating instruction is to maximize each student’s growth and individual success by meeting each student where he or she is, and assisting in the learning process." Educators who differentiate instruction strive to "recognize students varying background knowledge, readiness, language, preferences in learning, interests; and to react responsively" (Hall, Strangman, & Meyer, 2003, Definition section).
 As promoters of differentiated instruction, Carol Ann Tomlinson and Jay
McTighe (2006) indicated that it is primarily an instructional design model that
focuses on "whom we teach, where we teach, and how we teach" (p. 3).
Tomlinson is the author of
How to Differentiate Instruction in Academically Diverse Classrooms
(3rd ed.) 2017).
As promoters of differentiated instruction, Carol Ann Tomlinson and Jay
McTighe (2006) indicated that it is primarily an instructional design model that
focuses on "whom we teach, where we teach, and how we teach" (p. 3).
Tomlinson is the author of
How to Differentiate Instruction in Academically Diverse Classrooms
(3rd ed.) 2017).
The process of differentiation is challenging for educators, as it requires developing skills to teach in a flexible manner that responds to the unique needs of learners. Often total lessons or the pace of individual lessons need to be adjusted "on-the-fly." Teacher-led group instruction is only one model of instruction. So, teachers also need to know about additional resources beyond what's in the textbook or available in print format that can be used to help learners. For example, students can also learn from each other in collaborative groups, or from virtual instructors in online settings, or by working alone using software or apps. They can get different perspectives on a topic from viewing podcasts.
A second challenge for success lies in the teacher's ideological perspective, as this latter affects how one teaches. According to David Ferrero (2006), educators are divided by traditionalism and innovation. However, teaching that leads to achievement gains (e.g., via standardized testing) does not mean that educators have to choose between one or the other. There is a concept of "innovative traditionalism" that is student-centered, yet has been shown to improve standardized achievement test scores. This has been accomplished in two Chicago-area high schools by "a combination of test prep, classical content, and collaboratively developed thematic projects grounded in controversy and designed to cultivate student voice and civic engagement" (p. 11). The following table (Ferrero, 2006, p. 11) illustrates the essential differences in education's ideological divide, which can be bridged.
|
Education's Ideological Divide |
|
| Traditional | Innovative |
| Standardized tests | Authentic assessment |
| Basic skills | Higher-order thinking |
| Ability grouping | Heterogeneous grouping |
| Essays/research papers | Hands-on projects |
| Subject-matter disciplines | Interdisciplinary integration |
| Chronology/history | Thematic integration |
| Breadth | Depth |
| Academic mastery | Cultivation of individual talents |
| Eurocentrism | Multiculturalism |
| Canonical curriculum | Inclusive curriculum |
| Top-down curriculum | Teacher autonomy/creativity |
| Required content | Student interest |
|
Source: Ferrero, D. (2006). Having it all. Educational Leadership, 63(8), 11. https://www.ascd.org/el/articles/having-it-all |
|
The goals of differentiated instruction and innovative traditionalism are to ensure effective learning for all. Best practice learning adheres to 13 principles. Best practice is student-centered, experiential, holistic, authentic, expressive, reflective, social, collaborative, democratic, cognitive, developmental, constructivist, challenging with choices and students taking responsibility for their learning (Zemelman, Daniels, & Hyde, 1998, as cited in Wilcox & Wojnar, 2000).
According to Theroux (2004),
"Differentiating instruction means creating multiple paths so that students of different abilities, interest or learning needs experience equally appropriate ways to absorb, use, develop and present concepts as a part of the daily learning process. It allows students to take greater responsibility and ownership for their own learning, and provides opportunities for peer teaching and cooperative learning" (para. 2).
Theroux (2004) addressed four ways to differentiate instruction: content (requires pre-testing to determine the depth and complexity of the knowledge base that learners will explore), process (leads to a variety of activities and strategies to help students gain knowledge), product (complexity varies in ways for assessing learning), and manipulating the environment or accommodating learning styles. Fairness is a key concept to emphasize with learners, who will recognize that not everyone will work on the same thing at the same time. They need to appreciate that not everyone has the same needs.
Bottom Line:
Small and Lin (2022) noted a general agreement on how to effectivey implement differentiated instruction. Three elements are needed: a focus on teaching to the big Ideas, prior assessment to determine the needs that different students have, and student choice, whether in content, process, or product (Principles and Approaches to Differentiated Instruction section, para. 2).

The concept of differentiated instruction is not new. Historically it has been discussed in other terms related to addressing individual differences in instruction.
ASCD devoted its entire December 1953 issue of Educational Leadership to the theme "The Challenge of Individual Difference," which is available online. In the lead article, Adjusting the Program to the Child, Carleton Washburne presented a short history of reform efforts aimed at making education more individualized. What a find.
Read What Differentiated Instruction Really Means by Lisa Westman (2021, September 1) in ASCD.
In Creating a Differentiated Mathematics Classroom, Richard Strong, Ed Thomas, Matthew Perini, and Harvey Silver (2004) indicated that student differences in learning mathematics tend to cluster into four mathematical learning styles:
Mastery style--tend to work step-by-step
Understanding style--search for patterns, categories, reasons
Interpersonal style--tend to learn through conversation, personal relationship, and association
Self-Expressive style--tend to visualize and create images and pursue multiple strategies.
 Students can work in all four styles, but tend to develop
strengths in one or two of the styles. Each of these styles tends toward
one of four dimensions of mathematical learning: computation, explanation,
application, or problem solving. "If teachers incorporate all four styles
into a math unit, they will build in computation skills (Mastery), explanations
and proofs (Understanding), collaboration and real-world application
(Interpersonal), and nonroutine problem solving (Self-Expressive)" (p. 74).
Students can work in all four styles, but tend to develop
strengths in one or two of the styles. Each of these styles tends toward
one of four dimensions of mathematical learning: computation, explanation,
application, or problem solving. "If teachers incorporate all four styles
into a math unit, they will build in computation skills (Mastery), explanations
and proofs (Understanding), collaboration and real-world application
(Interpersonal), and nonroutine problem solving (Self-Expressive)" (p. 74).
 From an instructional styles perspective, Silver, Strong, and
Perini, authors of The strategic teacher:
Selecting the right research-based strategy for every lesson (2007), noted that teachers who use mastery strategies focus on increasing
students' abilities to remember and summarize. "They motivate by providing
a clear sequence, speedy feedback, and a strong sense of expanding competence
and measurable success." When focusing on interpersonal strategies,
teachers use "teams, partnerships, and coaching" to help students better relate
to the curriculum and each other. Understanding strategies help students
to reason and use evidence and logic. Teachers "motivate by arousing
curiosity using mysteries, problems, clues, and opportunities to analyze and
debate." Self-expressive strategies highlight students' imagination and
creativity. Teachers employ "imagery, metaphor, pattern, and what ifs to
motivate students' drive toward individuality and originality." Finally,
it's possible to use all four styles at the same time to achieve a balanced
approach to learning (Part One: Introduction section, Figure B).
From an instructional styles perspective, Silver, Strong, and
Perini, authors of The strategic teacher:
Selecting the right research-based strategy for every lesson (2007), noted that teachers who use mastery strategies focus on increasing
students' abilities to remember and summarize. "They motivate by providing
a clear sequence, speedy feedback, and a strong sense of expanding competence
and measurable success." When focusing on interpersonal strategies,
teachers use "teams, partnerships, and coaching" to help students better relate
to the curriculum and each other. Understanding strategies help students
to reason and use evidence and logic. Teachers "motivate by arousing
curiosity using mysteries, problems, clues, and opportunities to analyze and
debate." Self-expressive strategies highlight students' imagination and
creativity. Teachers employ "imagery, metaphor, pattern, and what ifs to
motivate students' drive toward individuality and originality." Finally,
it's possible to use all four styles at the same time to achieve a balanced
approach to learning (Part One: Introduction section, Figure B).
The implication for mathematics instruction is that "any sufficiently important mathematics topic requires students to learn the topic in four dimensions: procedurally, conceptually, contextually, and investigatively" (Strong et al., 2004, p. 75). Even taking that approach, we are challenged to help students overcome misconceptions.
Example:
The importance of addressing these four dimensions was made very clear in a recent query I had from an individual [let's call him Mac] seeking help for a learner in the 5th grade who was struggling to multiply decimal numbers. The learner had incorrectly calculated: 0.032 * 0.16 =0.0512. But why? Apparently the learner was taught an algorithm, but used it incorrectly. Let's examine the problem that arises in understanding if teaching is done only procedurally.
In investigating Web resources for Mac on this concept, several sites indicated using the algorithm with instructions to multiply the digits as whole numbers (here 32*16 = 512), then count up the number of decimal places indicated in the problem (here 5) and then to use that number of places in the final answer. If extra zeroes are needed (here 2), place them before the digits in the whole number answer. This kind of wording, which I purposely made less than mathematically precise, is what a 5th grader might typically remember from only an algorithm. Notice that the learner's answer (0.0512) did have five digits (places used incorrectly) and two zeroes preceding 512. The answer should have been 0.00512.
Conceptually, the learner might have missed a connection to prior learning on fractions, or the link was not made and reinforced in instruction. Writing the problem in its equivalent fraction form, using knowledge of converting decimals to fractions and vice versa, and decimal notation and place value might eventually have helped the learner to understand the short cut presented in the algorithm.

Contextually, understanding the position of the decimal point in the final answer might have been linked to an application problem, such as buying 2.6 yards of fabric at $1.75 per yard.
Investigatively, the learner might not have seen visual representations of the concept, such as the rectangle/area model for multiplication of decimals presented at Explore Learning.
In any case, the query confirmed Strong et al.'s (2004) recommendations and the need for differentiated instructional practices.

![]() For
a humorous take on the importance of developing conceptual understanding, watch the YouTube Video,
Ma and Pa
Kettle Math--they prove to you that 25 divided by 5 is 14!
For
a humorous take on the importance of developing conceptual understanding, watch the YouTube Video,
Ma and Pa
Kettle Math--they prove to you that 25 divided by 5 is 14!
![]() Sometimes
personal strategies for problem solving work better than algorithms.
Students who use them demonstrate conceptual understanding, as the YouTube
Video, Algorythm and Personal Strategies, illustrates.
Sometimes
personal strategies for problem solving work better than algorithms.
Students who use them demonstrate conceptual understanding, as the YouTube
Video, Algorythm and Personal Strategies, illustrates.
The example above noted teaching mathematical procedures using algorithms. Algorithms play an important role in mathematics, as they address step-by-step procedures for solving problems. According to the Advocates for the Science of Math (2021a), it's a misconception that algorithms promote memorization, contributing to "superficial understanding of steps, conventions, and rules. ... The truth is that "Using an algorithm requires conceptual understanding of what is happening in the problem and procedural knowledge to accurately solve. Algorithms can serve as a link between conceptual understanding and procedural knowledge."
For example, Everyday Mathematics includes algorithms, as explained at the University of Chicago. The difficulty arises, as the above example indicates, if the algorithm is taught without linking it to conceptual, contextual, and investigative understanding. Ball, Ferrini-Mundy, Kilpatrick, Milgram, Schmid, and Schaar (2005) indicated, "Fluent use and understanding ought to be developed concurrently." Algorithms not only play a role in gaining whole number computation fluency, but play a role in such examples as "constructing the bisector of an angle; solving two linear equations in two unknowns; calculating the square root of a number by a succession of dividing and averaging" (Areas of Agreement section).
According to Strong et al. (2004), testing practices should also aim to measure knowledge in all four dimensions. Teachers should be aware that texts and their accompanying tests, however, tend to emphasize only the mastery and understanding styles of learning. To differentiate instruction, teachers can:
Rotate strategies to appeal to students' dominant learning style and challenge them to work in their less preferred styles. Consider strategies such as using manipulatives, observing demonstrations, sketching out a math situation, reading, having students compare their work with a partner, or solving complex problems in a team.
Use flexible grouping.
Personalize/individualize learning for struggling students or for those needing an extra challenge.
Among strategies for implementing differentiated instruction, Tomlinson and McTighe (2006) suggested that teachers consider:
Compacting--giving students credit for what they already know;
Negotiated delay of due dates and times for tasks;
Varied homework;
Bookmarked Web sites on key topics in languages other than English to support English language learners;
Video and audio clips to support multiple intelligences and varied learning styles and disabilities;
Flexible grouping, "expert" groups, and interspersing lecture with group discussions;
Guided peer review;
Teaching with part-to-whole and whole-to-part emphasis;
Tiered assignments--used when all students need to know the same skill or concept;
Learning contracts;
Independent study/projects;
WebQuests and Web inquiries;
Learning centers--primarily used in elementary grades; and
Adjusting questions to accommodate levels in Bloom's Taxonomy.
 In Good Questions: Great Ways to Differentiate Mathematics Instruction
(2nd ed). Marian Small (2012) recognized, "It is not realistic for a teacher to try to
create 30 different instructional paths for 30 students, or even 6 different
paths for 6 groups of students. Because this is the perceived alternative
to one-size-fits-all teaching, instruction in mathematics is often not
differentiated. To differentiate instruction efficiently, teachers need
manageable strategies that meet the needs of most of their students at the same
time" (p. 6). This can be accomplished using just two core strategies:
open questions and parallel tasks, which are the focus in her book. These
core strategies are addressed for grade bands preK-2, 3-5, and 6-8 within each
math strand: number and operations, geometry, measurement, algebra, and data
analysis and probability. Per Small:
In Good Questions: Great Ways to Differentiate Mathematics Instruction
(2nd ed). Marian Small (2012) recognized, "It is not realistic for a teacher to try to
create 30 different instructional paths for 30 students, or even 6 different
paths for 6 groups of students. Because this is the perceived alternative
to one-size-fits-all teaching, instruction in mathematics is often not
differentiated. To differentiate instruction efficiently, teachers need
manageable strategies that meet the needs of most of their students at the same
time" (p. 6). This can be accomplished using just two core strategies:
open questions and parallel tasks, which are the focus in her book. These
core strategies are addressed for grade bands preK-2, 3-5, and 6-8 within each
math strand: number and operations, geometry, measurement, algebra, and data
analysis and probability. Per Small:
x x x x
x x x x
x x x x
Several strategies are illustrated for creating open questions:
Turning around a question. Give the answer and ask for the question. For example: 10 is a fraction of a number. What could the fraction and number be?
Asking for similarities and differences of two items: numbers, shapes, probabilities, graphs, measurements, and so on.
Replacing a number with a blank. For example, in a word problem involving addition to find the answer, students might fill in the blanks in the word problem with their own choices.
Creating a sentence: Students can create a sentence using given parameters, such a a given set of words and numbers.
Using "soft" words. Soft words add some ambiguity, yet open up the thinking process. For example, rather than asking students to create a triangle with a specific area, students might be asked to create two triangles whose areas are different, but close.
Changing the question. Teachers might take an existing question and turn it into an open question. For example, a text might have the question "A cookie has a diameter of 1.75 inches. Express the diameter as a fraction in simplest form." An associated open question might be "The diameter of a cookie is between 1 and 2 inches. Express the diameter as a fraction in two different ways." (p. 9)
 For the secondary level, Marian Small and Amy Lin elaborated on how to differentiate math
instruction in More Good Questions: Great Ways
to Differentiate Math Instruction at the Secondary Level, 2nd ed. (2022).
The text addresses five content strands: algebra and functions, number,
geometry, measurement, and statistics and probability. Within each,
the differentiating open questions and parallel tasks are presented for grade
bands 6-8 and 9-12. There's a focus on teaching to the "big ideas."
The eight standards of mathematical practice are also addressed.
For the secondary level, Marian Small and Amy Lin elaborated on how to differentiate math
instruction in More Good Questions: Great Ways
to Differentiate Math Instruction at the Secondary Level, 2nd ed. (2022).
The text addresses five content strands: algebra and functions, number,
geometry, measurement, and statistics and probability. Within each,
the differentiating open questions and parallel tasks are presented for grade
bands 6-8 and 9-12. There's a focus on teaching to the "big ideas."
The eight standards of mathematical practice are also addressed.
Differentiating math instruction is also accomplished by using math menus, which are options giving learners choices for demonstrating their knowledge. "The options can include problems, investigations, games, and other activities that promote students' understanding, support their reasoning, or provide practice with the content and skills they've been learning" (Burns, 2016, p. 41).
A math menu -- like courses in a restaurant -- is one format for offering options. You'll also find other phrases used, such as choice boards (which might look like tic-tac-toe boards), learning menus, or extension menus.
With so many strategies, Linda Gojak (2012), an NCTM President, offered the following questions about process, which can be helpful when deciding how to structure and present a lesson:
Some might not appreciate the true essence of cooperative learning, a feature employed in differentiating instruction. Learners are responsible for not just their own learning, but the learning of others. Shared learning leads to success for all, as each member of a learning group has a specific role to play in reaching a common goal. Successful groups include positive interdependence--if one fails, the entire group is affected. There is both individual and group accountability; although some work might be completed individually, some must be accomplished by group interactions. Typical strategies include think-pair-share, the jigsaw, and numbered heads. Collaborative learning structures and techniques might also include the three-step interview, focused listing to brainstorm or examine concepts and descriptions, structured problem solving, one-minute papers, paired annotations, guided reciprocal peer questioning, and send-a-problem.
Robert Slavin (2014), director of the Center for Research and Reform in Education, discussed five strategies to make cooperative learning powerful. He stated, "It is the "learning" in cooperative learning that is too often left out. But it needn't be. Using these five strategies, teachers can get the greatest benefit possible from cooperative learning and ensure that collaboration enhances learning" (para. 3):
Access the Peeragogy Handbook, which is a collection of techniques for collaborative learning and collaborative work. This handbook is a "living-document" created by a world-wide community of editors interested in peer-to-peer learning. The ideas can be applied in classrooms, in research, in business, and more.
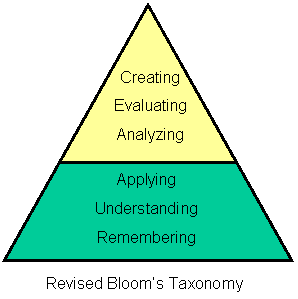 There
is more than one kind of learning. In 1956 Benjamin Bloom
identified three domains of learning: cognitive, affective, and psychomotor.
The cognitive domain focuses on knowledge or mental skills; the affective on the
growth of feelings, emotions, attitudes; and the psychomotor on manual or
physical skills (Clark, 2015). Within
Bloom's
Taxonomy of Learning Domains, the cognitive domain contains six levels:
knowledge, comprehension, application, analysis, synthesis and evaluation. The
taxonomy was later revised in the mid-90's and now has levels of remembering,
understanding, applying, analyzing, evaluating, and creating (Clark, 2015;
Forehand, 2005).
There
is more than one kind of learning. In 1956 Benjamin Bloom
identified three domains of learning: cognitive, affective, and psychomotor.
The cognitive domain focuses on knowledge or mental skills; the affective on the
growth of feelings, emotions, attitudes; and the psychomotor on manual or
physical skills (Clark, 2015). Within
Bloom's
Taxonomy of Learning Domains, the cognitive domain contains six levels:
knowledge, comprehension, application, analysis, synthesis and evaluation. The
taxonomy was later revised in the mid-90's and now has levels of remembering,
understanding, applying, analyzing, evaluating, and creating (Clark, 2015;
Forehand, 2005).
Students should work at all levels of the taxonomy. It should not be viewed as a ladder, however, nor as a framework for differentiated instruction (Tomlinson & McTighe, 2006, pp. 119-120). The taxonomy is helpful for breaking down state standards into meaningful components as teachers plan their instruction. Planning for instruction will be elaborated upon in Part 3 of this essay on content and curriculum mapping.
Charles White (2007) provided a closer look at how Bloom’s Taxonomy provides levels of understanding to guide teaching and assessing knowledge. Teaching for each level has different instructional strategies and testing techniques.
Knowledge: Memorization
and recitation fall within the knowledge level. Teachers might rely on a
lecture method and assigned readings. They are transmitters of knowledge. Students remain passive and acquire familiarity with the material, take
notes, memorize, and study enough so that they can recall information at
least long enough to pass tests, which might be multiple choice or
true/false. Such tests rely on one-right answer. “Opinions and values are
excluded from this type of testing” (p. 162). When writing, students tend to
parrot back what the teacher has said. However, the ability to recite
information that has been memorized does not mean that students know what
they are saying.
NOTE: Memorization does not come easy for learners, but some
memorization is involved in mathematics. For example, read
The Benefits
of Memorizing Math Facts by Margaret Groves (2010).
She stated, "Quite simply, a lack of
fluency in basic math fact recall significantly hinders a child's
subsequent progress with problem-solving, algebra and higher-order
math concepts. This can have a serious impact on a child's
overall self confidence and general academic performance" (para. 1).
Get some memorization tips/techniques and learn how to
improve your short and long-term memory at
Memorization Tips.
Comprehension: At a comprehension level, students are able to discuss what they’ve learned in their own words rather than in the teacher’s words, express their feelings, participate in classroom debate, and are thus taking ownership of content and remembering it better. They would be able to explain a graph, a calculation using a formula, or an equation (e.g., linear regression), but not necessarily be able to implement associated tools. At this level, “short- and medium-length answers [in students’ own words] combined with complex multiple-choice formats often serve as the medium of test material” (p. 162).
Application: While key words for comprehension are explaining and discussion, application involves doing. Novices lacking understanding might only be able to apply knowledge when given step-by-step instructions that can be used without deviation. However, at this level, students must be able to demonstrate that they can use concepts and theories in problem-solving. They might be given all the information necessary to do calculations or tasks. Memory at this level is enhanced with repetition. Testing includes unstructured problems that might not have been encountered in the text or during a lecture, requiring students to determine a solution method using what they have learned. Novice students might still turn to the teacher for a correct solution.
Analysis: At this level, application is taken a step further. Students must be able to take a situation apart, diagnose its pieces, and decide for themselves what tools (e.g., graph, calculation, formula, etc.) to apply to solve the problem at hand. Rather than just understanding and applying individual concepts, students understand the relationship among concepts. Case studies in business, for example, fit this level. The level of difficulty can be controlled for novices to experts by the number of issues presented in the cases requiring analysis. Likewise, this process to control difficulty can be used for any mathematics problem-solving scenario based on level of expertise of learners. For example, at elementary levels, students are introduced to analysis when a few extraneous facts are included in a problem, which are not needed to solve it. At an analysis level, students are able to appreciate that some problems do not have a unique solution and there is more than one way to defend a position or solution method, as in a case study.
Synthesis: In contrast to analysis (i.e., taking apart), at the synthesis level students put things back together. Given the pieces, there might be more than one way to do this. In terms of mathematics, students might take the pieces they’ve learned, and put them together to solve problems not yet encountered in the actual classroom setting. Synthesis is involved when creating something new. Advanced students might be asked to create a new theory. Synthesis is tested via major projects, for example, which might be long term involving creativity and application of all that students have learned on a topic.
Evaluation: Teachers evaluate student work all the time, particularly exams and homework. The difficulty in evaluation arises when judging multiple perspectives and varied problem-solving approaches, as one must be thoroughly familiar with content. At this level, students might be asked to problem-solve via debate, for example. At the evaluation level, one is able “to judge the work of others at any level of learning with regard to its accuracy, completeness, logic, and contribution” (White, 2007, p. 161). Rubrics help teachers to evaluate work, particularly for that involving application, analysis and synthesis.
White (2007) presented a novel way to test levels of understanding. He proposed writing two test questions on a topic, allowing students to choose only one of those to answer. The first is written for the knowledge and comprehension levels (e.g., key verbs: list, describe), and the second is written for the higher critical thinking levels of application, analysis, and synthesis. Points possible would be indicated for each, so that students would recognize that only those answering the second could be awarded maximum points toward an A+ grade. The option to choose enables the less able student to better demonstrate what he does know and perhaps earn a B grade, rather than risk failure because of an inability to demonstrate critical thinking. For either question, students could fail.
Bloom's Taxonomy Mathematics Chart includes verbs and sample tasks related to mathematics for each level of the taxonomy to help with curriculum planning.
Lesson Planning using Bloom's Taxonomy in my Math Classroom by Shalini Chauhan (2020, July 8) provides examples.
Bloomin' Apps: Kathy Shrock has gathered a collection of apps for each level in the revised Bloom's Taxonomy. They are arranged for iPad, Android, Online Tools, and for G Suite. Note: G Suite for Education is now known as Google Workspace for Education.
Krathwohl, D. (2002). A revision of Bloom’s taxonomy: An overview. Theory into Practice, 41(4), 212-219. https://www.depauw.edu/files/resources/krathwohl.pdf
You can learn more on the Revised Bloom's Taxonomy at the Iowa State University Center for Excellence in Learning and Teaching web site.
Join a Discussion Group or Participate in a Blog
 It's easy for teachers to discuss topics in education and math methodology with
colleagues around the world.
It's easy for teachers to discuss topics in education and math methodology with
colleagues around the world.
Here's some blogs for math educators:
See other blog options for math educators noted in our technology integration resources.
Back to top | Math Methodology Instruction Essay: Page 1 | 2 | 3
114th Congress of the United States. (2015). Every Student Succeeds Act. https://www.ed.gov/essa
Advocates for the Science of Math. (2021a). Common misconceptions: Algorithms. https://www.thescienceofmath.com/misconceptions-algorithms
Advocates for the Science of Math. (2021b). Common misconceptions: Growth mindset increases math achievement. https://www.thescienceofmath.com/misconceptions-growth-mindset-increases-math-achievement
American Psychological Association, Coalition for Psychology in Schools and Education. (2015). Top 20 principles from psychology for preK–12 teaching and learning. https://www.apa.org/ed/schools/teaching-learning/top-twenty-principles.pdf
Anderson, M. (2021, December 6). 6 intrinsic motivators to power up your teaching. Educational Leadership, 79(4). https://www.ascd.org/el/articles/6-intrinsic-motivators-to-power-up-your-teaching
Ball, D. L., Ferrini-Mundy, J., Kilpatrick, J., Milgram, R. J., Schmid, W., & Schaar, R. (2005). Reaching for common ground in K-12 mathematics education. Notices of the AMS, 52(9), 1055-1058. https://www.ams.org/notices/200509/comm-schmid.pdf
Boser, U. (2019). What do teachers know about the science of learning? https://www.the-learning-agency.com/insights/what-do-teachers-know-about-the-science-of-learning
Breaux, E. (2009). How the best teachers avoid the 20 most common teaching mistakes. Larchmont, NY: Eye on Education. Available: https://amzn.to/3FSaR9N
Burns, M. (2016). Using math menus. Educational Leadership, 74(2), 40-44. https://www.ascd.org/el/articles/using-math-menus
Centre for Education Statistics and Evaluation. (2017, August). Cognitive load theory: Research that teachers really need to understand. New South Wales, Australia: Author. https://www.cese.nsw.gov.au/publications-filter/cognitive-load-theory-research-that-teachers-really-need-to-understand
Charles A. Dana Center at The University of Texas at Austin, & the Collaborative for Academic, Social, and Emotional Learning. (2016). Integrating social and emotional learning and the Common Core Standards for Mathematics: Making the case. https://www.insidemathematics.org/sites/default/files/assets/common-core-resources/social-emotional-learning/a__integrating_sel_and_ccssm_making_the_case.pdf
Clark, D. (2015). Bloom's taxonomy of learning domains. http://knowledgejump.com/hrd/bloom.html
Coe, R., Aloisi, C., Higgins, S., & Elliot Major, L. (2014, October). What makes great teaching? London, UK: The Sutton Trust. https://www.suttontrust.com/research-paper/great-teaching/
Common Core State Standards. (2010). Standards for Mathematical Practice. Washington, DC: National Governors Association Center for Best Practices, Council of Chief State School Officers. https://www.thecorestandards.org/Math/Practice/
Connecticut State Department of Education. (2010). 2010 Common core of teaching: Foundational skills. Hartford, CT: Author. https://portal.ct.gov/-/media/CA1519B5964A47DBA11BC29CE99E857E.pdf?la=en
Council of Chief State School Officers. (2011). Interstate teacher assessment and support consortium (InTASC) model core teaching standards: A resource for state dialogue. Washington, DC: Author. https://ccsso.org/resource-library/intasc-model-core-teaching-standards [Note: this document was updated 2017.]
Cuban, L. (2019, October 8). Whatever happened to Madeline Hunter? [Blog post]. https://larrycuban.wordpress.com/2019/10/08/whatever-happened-to-madeline-hunter-lesson-plans/
Danielson, C. (2007). Enhancing professional practice: A framework for teaching (2nd ed.). Alexandria, VA: ASCD. Available: https://amzn.to/3O1yIZ4
Deans for Impact. (2015). The Science of Learning. Austin, TX: Deans for Impact. https://deansforimpact.org/wp-content/uploads/2016/12/The_Science_of_Learning.pdf
Dembo, M., & Howard, K. (2007). Advice about the use of learning styles: A major myth in education. Journal of College Reading and Learning, 37(2), 101-109. https://eric.ed.gov/?id=EJ767768
Drake, C. (2016, March 3). The fantastic new ways to teach math that most schools aren't even using [Opinion]. https://hechingerreport.org/the-fantastic-new-ways-to-teach-math-that-most-schools-arent-even-using/
Dweck, C. (2015, September 22). Carol Dweck revisits growth mindset. Education Week, 35(5), 20, 24. https://www.edweek.org/leadership/opinion-carol-dweck-revisits-the-growth-mindset/2015/09
Dynarski, M. (2015, December 10). Using research to improve education under the Every Student Succeeds Act. https://www.brookings.edu/research/using-research-to-improve-education-under-the-every-student-succeeds-act/
Ferrero, D. (2006). Having it all. Educational Leadership, 63(8), 8-14. https://www.ascd.org/el/articles/having-it-all
Finster, M., Decker-Woodrow, L., Booker, B., Mason, C. A., Tu, S., & Lee, J. (2023). Cost-effectiveness of algebraic technological applications. Journal of Research on Eduational Effectiveness. https://www.tandfonline.com/doi/full/10.1080/19345747.2023.2269918
Fletcher-Wood, H. (2022, March 6). Is growth mindset real? New evidence, new conclusions [Blog post]. https://improvingteaching.co.uk/2022/03/06/is-growth-mindset-real-new-evidence-new-conclusions/
Forehand, M. (2005). Bloom's taxonomy: Original and revised. In M. Orey (Ed.), Emerging perspectives on learning, teaching, and technology. http://epltt.coe.uga.edu/index.php?title=Main_Page
Gojak, L. M. (2012, October 3). To flip or not to flip: That is not the question! NCTM Summing Up. https://www.nctm.org/News-and-Calendar/Messages-from-the-President/Archive/Linda-M_-Gojak/To-Flip-or-Not-to-Flip_-That-Is-NOT-the-Question!/
Goodwin, B. (2010). Choice is a matter of degree. Educational Leadership, 68(1), 80-81. https://www.ascd.org/el/articles/choice-is-a-matter-of-degree
Groves, M. (2010). The benefits of memorizing math facts. Portland, OR: QuickReckoning, Inc. http://quickreckoning.com/math_research.htm
Hall, T., Strangman, N., & Meyer, A. (2003). Differentiated instruction and implications for UDL implementation. Wakefield, MA: National Center on Accessing the General Curriculum. https://sde.ok.gov/sites/ok.gov.sde/files/DI_UDL.pdf
Hattie, J. (2003, October). Teachers make a difference: What is the research evidence? Paper presented at the Australian Council for Educational Research Annual Conference on Building Teacher Quality, Melbourne. https://www.educationalleaders.govt.nz/Pedagogy-and-assessment/Building-effective-learning-environments/Teachers-Make-a-Difference-What-is-the-Research-Evidence
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students' learning. In F. K. Lester (Ed.), Second Handbook of Research on Mathematics Teaching and Learning (pp. 371-404). https://web.archive.org/web/20210417124003/https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.405.3591&rep=rep1&type=pdf
Hoerr, T. (2013). Fostering grit: How do I prepare my students for the real world? Alexandria, VA: ASCD. Available: https://amzn.to/3tG3gIZ
Immordino-Yang, M. H. (2016). Emotions, learning, and the Brain: Exploring the educational implications of affective neuroscience. New York: W. W. Norton & Company. Available: https://amzn.to/48vUr3h
Kini, T., & Podolsky, A. (2016). Does teaching experience increase teacher effectiveness?: A review of the research. Palo Alto, CA: Learning Policy Institute. https://learningpolicyinstitute.org/our-work/publications-resources/does-teaching-experience-increase-teacher-effectiveness-review-research
Kratochwill, T. (n.d.). Classroom management: Teachers modules. Washington, DC: American Psychological Association. https://www.apa.org/education/k12/modules-classroom-management
Malouff, J. (2018). Over 50 problem solving strategies explained. University of New England Blog. https://blog.une.edu.au/usingpsychology/2018/10/15/over-fifty-problem-solving-strategies-explained/
Mandel, S. (2006). What new teachers really need. Educational Leadership, 63(6), 66-69. https://www.ascd.org/el/articles/what-new-teachers-really-need
Marzano, R. (2010). Art and science of teaching/ High expectations for all. Educational Leadership, 68(1), 82-84. https://www.ascd.org/el/articles/high-expectations-for-all-sept-2010
Marzano, R. (2011). Art and science of teaching/ Relating to students: It's what you do that counts. Educational Leadership, 68(6), 82-83. https://www.ascd.org/el/articles/relating-to-students-its-what-you-do-that-counts
Marzano, R., Marzano, J., & Pickering, D. (2003). Classroom management that works: Research-based strategies for every teacher. Alexandria, VA: ASCD. Available: https://amzn.to/3u4q5Wi
McConachie, S., Hall, M., Resnick, L., Ravi, A., Bill, V., Bintz, J., & Taylor, J. (2006). Task, text, and talk: Literacy for all subjects. Educational Leadership, 64(2), 8-14. https://www.ascd.org/el/articles/task-text-and-talk-literacy-for-all-subjects
Mehrotra, P. (2019, June 4). Five simple ways to add creativity in mathematics. https://www.edcircuit.com/five-simple-ways-to-add-creativity-in-mathematics/
Moran, S., Kornhaber, M., & Gardner, H. (2006). Orchestrating multiple intelligences. Educational Leadership, 64(1), 23-27. https://www.ascd.org/el/articles/orchestrating-multiple-intelligences
Muschla, J., Muschla, G., & Muschla-Berry, E. (2013). Math starters: 5- to 10-minute activities aligned with the Common Core math standards, grades 6-12 (2nd Ed.). San Francisco, CA: Jossey-Bass. Available: https://amzn.to/47MLOAx
National Academies of Sciences, Engineering, and Medicine. (2018). How people learn II: Learners, contexts, and cultures. Washington, DC: The National Academies Press. https://www.nap.edu/catalog/24783/how-people-learn-ii-learners-contexts-and-cultures
National Board for Professional Teaching Standards. (2002). What teachers should know and be able to do: The five core propositions of the national board. https://www.nbpts.org/standards-five-core-propositions/
National Council of Teachers of Mathematics. (2024, February). Position statement: Artificial intelligence and mathematics teaching. https://www.nctm.org/standards-and-positions/Position-Statements/Artificial-Intelligence-and-Mathematics-Teaching/
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all, Executive summary. Reston, VA: Author. https://www.nctm.org/PtA/
Newton, P., & Salvi, A. (2020, December 14). How common is belief in the learning styles neuromyth, and does it matter? A pragmatic systematic review. Frontiers in Education. https://www.frontiersin.org/articles/10.3389/feduc.2020.602451/full
November, A. (2016, June 13). The 7 questions every new teacher should be able to answer. https://www.eschoolnews.com/2016/06/13/the-7-questions-every-new-teacher-should-be-able-to-answer/
Omotayo, S.A., & Adeleke, J.O. (2017). The 5E instructional model: A constructivist approach for enhancing students' learning outcomes in mathematics. Journal of the International Society for Teachr Education, 21(2), 15-26. https://files.eric.ed.gov/fulltext/EJ1176946.pdf
O'Shea, M. (2005). From standards to success. Alexandria, VA: ASCD. Available: https://amzn.to/3TVl3Xi
Pashler, H., McDaniel, M., Rohrer, D., & Bjork, R. (2009). Learning styles: Concepts and evidence. Psychological Science in the Public Interest, 9(3), 105-119. doi: 10.1111/j.1539-6053.2009.01038.x https://www.psychologicalscience.org/journals/pspi/PSPI_9_3.pdf
Patek, A. (2019, August 14). Why using a behavior chart is ineffective. http://web.archive.org/web/20230202110507/https://genmindful.com/blogs/mindful-moments/behavioral-charts-i-am-totally-over-it
PBS & Grunwald Associates LLC. (2009). Digitally inclined. https://www.grunwald.com/pdfs/Grunwald_January_2010_ANNUAL_PBS_SURVEY_PUBLIC_REPORT.pdf
Polikoff, M.S., Petrilli, M.J., & Loveless, T. (2020). A decade on, has Common Core failed? Assessing the impact of national standards. Education Next, 20(2), 72-81. https://www.educationnext.org/wp-content/uploads/2022/01/ednext_XX_2_forum.pdf
Pollock, J. E. (2007). Improving student learning one teacher at a time. Alexandria, VA: ASCD. Available: https://amzn.to/47w3vny
Popham, W. J. (2009). Instruction that measures up: Successful teaching in the age of accountability. Alexandria, VA: ASCD. https://www.ascd.org/books/instruction-that-measures-up
Prashnig, B. (2005, Autumn). Learning styles vs. multiple intelligences. Teaching Expertise Magazine, issue 9. https://www.creativelearningcentre.com/downloads/LS%20vs%20MI%20TEX9_p8_9.pdf
Responsive Classroom web site. (2016, 2021). About: Principles & Practices. https://www.responsiveclassroom.org/about/principles-practices/ Note: the 2016 page is available at http://web.archive.org/web/20160124134005/https://www.responsiveclassroom.org/about/principles-practices/
Rutgers University. (n.d.). Diversity and inclusion initiatives: About section. http://inclusion.rutgers.edu/about-the-campaign/
Schmoker, M. (2006). Results now. Alexandria, VA: ASCD.
Silver, H., Strong, R., & Perini, M. (2007). The strategic teacher: Selecting the right research-based strategy for every lesson. Alexandria, VA: ASCD. Available: https://amzn.to/41Roq3r
Slavin, R. (2014). Making cooperative learning powerful. Educational Leadership, 72(2), 22-26. https://www.ascd.org/el/articles/making-cooperative-learning-powerful
Slavin, R. (2019, September 12). What kinds of teacher knowledge matter most? Robert Slavin's Blog. https://robertslavinsblog.wordpress.com/2019/09/12/what-kinds-of-teacher-knowledge-matter-most/
Small, M. (2012). Good questions: Great ways to differentiate mathematics instruction, 2nd ed. New York: Teachers College Press, and Reston, VA: National Council of Teachers of Mathematics. Available: https://amzn.to/47BvYIC
Small, M., & Lin, A. (2022). More good questions: Great ways to differentiate math Instruction at the secondary level, 2nd ed. New York: Teachers College Press, and Reston, VA: National Council of Teachers of Mathematics. Available: https://amzn.to/3KY0DYH
Smith, M. K. (2001). David Kolb on learning styles. The Encyclopedia of Informal Education. https://www.infed.org/biblio/b-explrn.htm#learning%20style. Last updated: August 23, 2007.
Smith, M. K. (2002, 2008). Howard Gardner and multiple intelligences. The Encyclopedia of Informal Education. https://infed.org/mobi/howard-gardner-multiple-intelligences-and-education/
Sornson, B. (2010, September 2). Mastering classroom management. ASCD Express, 5(24). https://www.ascd.org/el/articles/mastering-classroom-management
Sparks, S. (2019, April 3). Brain science backs up the role of "mindset" in motivating students for math. Education Week Leadership. https://www.edweek.org/leadership/brain-science-backs-up-role-of-mindset-in-motivating-students-for-math/2019/04
Steele, C. F. (2009). Inspired teacher: How to know one, grow one, or be one. Alexandria, VA: ASCD. https://www.ascd.org/books/the-inspired-teacher
Stigler, J. W., & Hiebert, J. (2004). Improving mathematics teaching. Educational Leadership, 61(5), 12-17. https://www.ascd.org/el/articles/improving-mathematics-teaching
Strauss, V. (2013, October 16). Howard Gardner: ‘Multiple intelligences’ are not ‘learning styles'. Washington Post. https://www.washingtonpost.com/news/answer-sheet/wp/2013/10/16/howard-gardner-multiple-intelligences-are-not-learning-styles/
Strong, R., Thomas, E., Perini, M., & Silver, H. (2004). Creating a differentiated mathematics classroom. Educational Leadership, 61(5), 73-78. https://www.ascd.org/el/articles/creating-a-differentiated-mathematics-classroom
Stronge, J., Straessle, J., & Xu, X. (2023). Smart from the start: 100 tools for teaching with confidence. Alexandria, VA: ASCD. Available: https://amzn.to/3skzLv5
Sullo, B. (2009). The motivated student: Unlocking the enthusiasm for learning. Alexandria, VA: ASCD. Available: https://amzn.to/3P1H6IF
The IRIS Center. (2017). High-quality mathematics instruction: What teachers should know. https://iris.peabody.vanderbilt.edu/module/math/
Theroux, P. (2004). Differentiating instruction. Alberta, CA: Enhance Learning with Technology Web site. Available archived from https://web.archive.org/web/20170218010740/http://members.shaw.ca/priscillatheroux/differentiating.html
Tomlinson, C., & McTighe, J. (2006). Integrating differentiated instruction & Understanding by Design. Alexandria, VA: ASCD. Available: https://amzn.to/3uGP1DA
Voltz, D., Sims, M., & Nelson, B. (2010). Connecting teachers, students, and standards: Strategies for success in diverse and inclusive classrooms. Alexandria, VA: ASCD. https://amzn.to/48H5c2M
White, C. (2007, January/February). Levels of understanding: A guide to the teaching and assessment of knowledge. Journal of Education for Business, 82(3), 159-163.
Wilcox, B. L., & Wojnar, L. C. (2000, August). Best practice goes online. Reading Online, 4(2). https://eric.ed.gov/?id=ED444117 or https://web.archive.org/web/20001202095700/http://www.readingonline.org/articles/art_index.asp?HREF=/articles/wilcox/index.html
Willingham, D. T. (2009-2010, Winter). Ask the cognitive scientist: Is it true that some people just can't do math? American Educator, 14-19, 39. https://www.aft.org/sites/default/files/willingham.pdf
Willingham, D. T. (2018). Ask the cognitive scientist: Does tailoring instruction to "learning styles" help students learn? American Educator, 42(2), 28-36. https://www.aft.org/ae/summer2018/willingham
Willingham, D., Hughes, E., & Dobolyi, D. (2015). The scientific status of learning styles theories. Teaching of Psychology, 42(3), 266-271. https://www.researchgate.net/publication/278666610_The_Scientific_Status_of_Learning_Styles_Theories
Zhang, L., & Sternberg, R. (2005, March). A threefold model of intellectual styles. Educational Psychology Review, 17(1), 1-53. https://www.researchgate.net/publication/226432426_A_Threefold_Model_of_Intellectual_Styles
Back to top | Math Methodology Instruction Essay: Page 1 | 2 | 3
![]() See
other Math Methodology pages:
See
other Math Methodology pages:
Instruction--Resources, Assessment and Curriculum: Content and Mapping