Math Topics
Learning Support
Professional
![]()
 Math Methodology is a three part series on instruction,
assessment, and curriculum. Sections contains relevant essays and
resources:
Math Methodology is a three part series on instruction,
assessment, and curriculum. Sections contains relevant essays and
resources:
Part 1: Math Methodology: Instruction
Part 2: Math Methodology: Assessment essay and resources
Part 3: Curriculum: Content and Mapping and resources
![]()
 Although learning for understanding is unique to an individual, teachers
can enhance the process of learning with their own knowledge of how people
learn. The National Research Council (2005) stated three fundamental and
well-established principles of learning, which all teachers should
understand and address in their teaching:
Although learning for understanding is unique to an individual, teachers
can enhance the process of learning with their own knowledge of how people
learn. The National Research Council (2005) stated three fundamental and
well-established principles of learning, which all teachers should
understand and address in their teaching:
 Research has shown that "metacognitive and cognitive abilities are not
naturally endowed" (Wilson & Conyers, 2016, p. 8). Educators should not
assume that students will naturally acquire metacognitive (i.e., thinking about
one's thinking) strategies for learning, as they delve into their courses. They must be explicitly taught
and learners will need intensive practice for when, how, where, and why to use
them (pp. 7-8). Wilson and Conyers provide such strategies in
Teaching
Students to Drive Their Brains: Metacognitive Strategies, Activities, and Lesson Ideas.
Research has shown that "metacognitive and cognitive abilities are not
naturally endowed" (Wilson & Conyers, 2016, p. 8). Educators should not
assume that students will naturally acquire metacognitive (i.e., thinking about
one's thinking) strategies for learning, as they delve into their courses. They must be explicitly taught
and learners will need intensive practice for when, how, where, and why to use
them (pp. 7-8). Wilson and Conyers provide such strategies in
Teaching
Students to Drive Their Brains: Metacognitive Strategies, Activities, and Lesson Ideas.
In their introduction to mathematical understanding, Karen Fuson, Mindy Kalchman, and John Bransford (National Research Council, 2005, pp. 217-256) noted some of the preconceptions that students might have about mathematics: Mathematics is about learning to compute; Mathematics is about "following rules" to guarantee correct answers; and, Some people have the ability to "do math" and others don't. Teachers must engage those, as they can be counterproductive to learning and contribute to students' lack of desire to study mathematics.
As mathematics educators, we want our learners ultimately to be mathematically literate and proficient in mathematics. To achieve this, educators will need to focus on deeper learning and learning for understanding. By deeper learning, we mean "the process through which a person becomes capable of taking what was learned in one situation and applying it to new situations – in other words, learning for “transfer.” Through deeper learning, students develop expertise in a particular discipline or subject area" (National Research Council, 2012, p. 1). It involves six "competencies students must master in order to develop a keen understanding of academic content and apply their knowledge to problems in the classroom and on the job. [Students must] master core academic content, think critically and solve complex problems, communicate effectively, work collaboratively, learn how to learn, [and] develop academic mindsets" (Hewlett Foundation, 2013).
Volker Ulm (2011) noted that mathematical literacy involves several competencies:
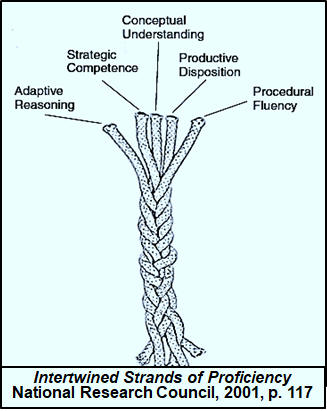 Developing proficiency, as the National
Research Council (2001) pointed out, embodies "expertise, competence, knowledge,
and facility in mathematics" and the term mathematical proficiency
entails what is "necessary for anyone to learn mathematics successfully" (p. 116).
It has five interwoven and interdependent strands:
Developing proficiency, as the National
Research Council (2001) pointed out, embodies "expertise, competence, knowledge,
and facility in mathematics" and the term mathematical proficiency
entails what is "necessary for anyone to learn mathematics successfully" (p. 116).
It has five interwoven and interdependent strands:
conceptual understanding—comprehension of mathematical concepts, operations, and relations [Note: for more on conceptual understanding, read Conceptual Understanding in Mathematics by Grant Wiggins (2014).]
procedural fluency—skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
strategic competence—ability to formulate, represent, and solve mathematical problems
adaptive reasoning—capacity for logical thought, reflection, explanation, and justification
productive disposition—habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy. (National Research Council, 2001, p. 116)
Becoming mathematically literate and proficient are ongoing processes. Writing in IAE-pedia, David Morsund and Dick Ricketts (2010) noted that becoming proficient is a matter of developing math maturity, which certainly varies among students and which involves how well they learn and understand the math, how well they can apply their knowledge and skills in a variety of math-related problem-solving situations, and in their long term retention.
While teachers have a role to play in helping students to develop understanding, students also have a role to play in the process, which cannot be overlooked. They must have intrinsic motivation, as in Eric Booth's (2013) words: "Learning can be transformed into understanding only with intrinsic motivation. Learners must make an internal shift; they must choose to invest themselves to truly learn and understand" (p. 23). This kind of motivation involves fulfilling their need for creative engagement, which is where the teacher's role in the design of instruction and corresponding assessments comes into play.
Understanding "typically entails being able to explain processes and relationships, apply conceptual knowledge to new situations, and interpret ideas in intended ways" (Zwiers, O'Hara, & Pritchard, 2014, p. 210). In mathematics, understanding goes beyond just getting the right answer to a problem. Students develop many misconceptions over time, which must be addressed in instruction. There are multiple examples to illustrate the problem.
 Deborah Schifter and Susan Jo Russell (2014/2015) noted elementary students
might incorrectly subtract if regrouping is needed as in writing 46 - 18 = 32
because 4 - 1 = 3 and 8 - 6 = 2.
They might not understand that, unlike in addition,
subtraction is not commutative. Or, they might incorrectly multiply 16 x 18 as (10 x 10) + (6 x 8)
because they learned in addition you can add the tens, add the ones, and add the result
as in 16 + 18 --so why not in multiplication? Eventually, they might misinterpret the distributive
property and write 2(3 x 5) as (2 x 3) x (2 x 5). The misconception
might transfer into algebra. For example, they might write 2(ab) = (2a) (2b). Schifter
and Russell illustrated the value of students modeling problems with such examples and then describing their
observations to help overcome misconceptions. They stated:
Deborah Schifter and Susan Jo Russell (2014/2015) noted elementary students
might incorrectly subtract if regrouping is needed as in writing 46 - 18 = 32
because 4 - 1 = 3 and 8 - 6 = 2.
They might not understand that, unlike in addition,
subtraction is not commutative. Or, they might incorrectly multiply 16 x 18 as (10 x 10) + (6 x 8)
because they learned in addition you can add the tens, add the ones, and add the result
as in 16 + 18 --so why not in multiplication? Eventually, they might misinterpret the distributive
property and write 2(3 x 5) as (2 x 3) x (2 x 5). The misconception
might transfer into algebra. For example, they might write 2(ab) = (2a) (2b). Schifter
and Russell illustrated the value of students modeling problems with such examples and then describing their
observations to help overcome misconceptions. They stated:
Deep understanding of arithmetic, central to the K-5 curriculum, rests on three pillars:
- Understanding numbers includes understanding written and oral counting; the structure of the base ten system with whole numbers and decimals; and the meaning of fractions, zero, and quantities less than zero.
- Developing computational fluency includes building a repertoire of accurate, efficient, and flexible strategies for each operation and knowing how and when to apply them.
- Examining the behavior of the operations includes modeling these operations, describing and justifying behaviors that are consequences of those properties, and comparing and contrasting the behaviors of different operations. (Three Pillars section)
Schifter and Russell together with Virginia Bastable are authors of Connecting Arithmetic to Algebra (Professional Book): Strategies for Building Algebraic Thinking in the Elementary Grades (2011).
 In Math
Misconceptions, PreK-Grade 5: From Misunderstanding to Deep Understanding
Bamberger, Oberdoff, and Schultz-Ferrell (2010) noted a range of similar
misconceptions that elementary students might bring to the classroom in number
and operations, algebra, geometry, measurement, data analysis and probability.
Students might believe adding fractions is done by adding the numerators and
adding the denominators and not understand the role of a common denominator.
They might believe adding a zero after a number "adds nothing." When comparing decimals less than one,
they might conclude that the decimal with the most digits is
larger. They might believe that you can't compute areas of circles using
"square" units, or that a square is not a rectangle because of its shape.
Fortunately for educators, the authors provide practical strategies and
activities to overcome a range of misconceptions. The key is to
consistently probe their understanding and provide them opportunities to show
and explain their reasoning.
In Math
Misconceptions, PreK-Grade 5: From Misunderstanding to Deep Understanding
Bamberger, Oberdoff, and Schultz-Ferrell (2010) noted a range of similar
misconceptions that elementary students might bring to the classroom in number
and operations, algebra, geometry, measurement, data analysis and probability.
Students might believe adding fractions is done by adding the numerators and
adding the denominators and not understand the role of a common denominator.
They might believe adding a zero after a number "adds nothing." When comparing decimals less than one,
they might conclude that the decimal with the most digits is
larger. They might believe that you can't compute areas of circles using
"square" units, or that a square is not a rectangle because of its shape.
Fortunately for educators, the authors provide practical strategies and
activities to overcome a range of misconceptions. The key is to
consistently probe their understanding and provide them opportunities to show
and explain their reasoning.
Consider misconceptions in the following. Have you ever heard students say (or have you as the teacher said), "To multiply by 10, just add a zero after the number"? Or, "The product of two numbers is always bigger than either one"? How about, "The number with the most digits is the biggest." Without an exploration of place value, students might not fully understand the role of "0" and believe that 9.07 = 9.7 or 5.40 < 5.400. In teaching operations with fractions, students learn when multiplying fractions to multiply the numerators and multiply the denominators as in 2/3 x 4/5 = 8/15. So, they might then incorrectly assume you can do the same when adding or subtracting fractions, as in 2/3 + 4/5 = 6/8. Using manipulatives might help to overcome such fraction misconceptions. Then consider learning about ratios and rates. Students might incorrectly believe "4:4" or "4 to 4" means 1.
Marilyn Burns (2014) suggested the importance of exploring the "why" in mathematics, as misconceptions might be uncovered in doing so. For example, if one is teaching elementary math topics, consider questions like "Why is it OK to add a zero when multiplying whole numbers by 10 but not when multiplying decimals by 10? Why is the sum of two odd numbers always even? Why is zero an even number? Why does canceling zeros produce an equivalent fraction in the fraction 10/20, but not in the fraction 101/201?" Such questions and misconceptions also set the tone for the need to teach mathematics right the first time with a focus on understanding.
In Wayne Snyder's (2013) view, "Without eliciting the mathematical thinking that lies behind the answer, there is no way to tell where understanding breaks down. Only by providing the structure, environment, and opportunity for students to share the reasoning behind their answers can we dislodge misconceptions" (para. 7). Further, reasoning is a cornerstone to understanding:
Eliciting students' thinking is not just about determining their misconceptions; it is also about understanding and encouraging their correct mathematical reasoning. ... Mathematical reasoning is a required part of the new paradigm of mathematics education, underscored and made explicit in the Common Core Standards for Mathematical Practice. Reasoning does not take the place of mathematical processes; rather, it strengthens the understanding, retention, and application of processes. Teaching for mathematical reasoning involves allowing and requiring students to express and to share their reasoning; listening to their explanations; and responding, guiding, and celebrating their mathematical thinking. (para. 9-10)
A focus on understanding is among key instructional shifts for implementing the Common Core State Standards. Certainly, understanding is an element of proficiency and literacy. While procedural skills and fluency are among those shifts with students being expected to have "speed and accuracy in calculation," for deep conceptual understanding, teachers are expected to teach more than how to get the answer and instead support students’ ability "to access concepts from a number of perspectives in order to see math as more than a set of mnemonics or discrete procedures." Further, teachers will need to ensure that students can correctly apply mathematics knowledge in new situations, which "depends on students having a solid conceptual understanding and procedural fluency"(Common Core State Standard Initiative: Shifts in Mathematics, 2010).
This is not to negate the role of memorization in mathematics. Morsund and Ricketts (2010) also noted, "It is well recognized that some rote memory learning is quite important in math education. However, most of this rote learning suffers from a lack of long term retention and from the learner’s inability to transfer this learning to new, challenging problem situations both within the discipline of math and to math-related problem situations outside the discipline of math. Thus, math education (as well as education in other disciplines) has moved in the direction of placing much more emphasis on learning for understanding. There is substantial emphasis on learning some “big ideas” that will last a lifetime" (section 1.1: Math Maturity, para. 1-2).
Barry Garelick (in Hess, 2021) offers a slightly different perspective. Although the "prevailing belief in current math-reform circles is that drilling kills the soul and makes students hate math and that memorizing the facts obscures understanding," he notes "there are some things in math that need to be memorized and drilled, such as addition and multiplication facts. Repetitive practice lies at the heart of mastery of almost every discipline, and mathematics is no exception. No sensible person would suggest eliminating drills from sports, music, or dance. De-emphasize skill and memorization and you take away the child’s primary scaffold for understanding" (para. 2, 3).
 Cheryl Rose Tobey and co-authors Carolyn Arline or Emily Fagan have written
four books, each for a grade band, on Uncovering Student Thinking About Mathematics
in the Common Core to
help uncover common math misconceptions related to the Common Core math
standards. Each book is similarly titled. For example, the high school book is
Uncovering Student Thinking About Mathematics in the Common Core, High School: 25 Formative Assessment Probes.
Others are for grades K-2,
3-5, and
6-8. Each book includes diagnostic questions, called formative assessment probes, designed to
help educators to then "systematically address conceptual and procedural
mistakes," identify struggling learners, and better plan for instruction
targeted to mastery of grade level Common Core standards.
Cheryl Rose Tobey and co-authors Carolyn Arline or Emily Fagan have written
four books, each for a grade band, on Uncovering Student Thinking About Mathematics
in the Common Core to
help uncover common math misconceptions related to the Common Core math
standards. Each book is similarly titled. For example, the high school book is
Uncovering Student Thinking About Mathematics in the Common Core, High School: 25 Formative Assessment Probes.
Others are for grades K-2,
3-5, and
6-8. Each book includes diagnostic questions, called formative assessment probes, designed to
help educators to then "systematically address conceptual and procedural
mistakes," identify struggling learners, and better plan for instruction
targeted to mastery of grade level Common Core standards.
Teachers play a significant role in how they plan for instruction and the strategies they use to help learners become mathematically literate and proficient. Per Fuson, Kalchman, and Bransford (in National Research Council, 2005):
"Developing mathematical proficiency requires that students master both the concepts and procedural skills needed to reason and solve problems effectively in a particular domain. Deciding which advanced methods all students should learn to attain proficiency is a policy matter involving judgments about how to use scarce instructional time" (p. 232). Teachers need to maintain a balance "between learner-centered and knowledge-centered needs. The learning path of the class must also continually relate to individual learner knowledge" (p. 235).
 A central
strategy for developing mathematical literacy is "enabling
students to find their own independent approaches to learning" (Ulm,
2011, p. 5). Along the way, students will make mistakes and
educators must acknowledge the role that mistakes have for achieving
engagement and learning. In the view of educator Miriam Clifford (2012), "Changing
the way we see errors and the time it takes to learn can help us produce better
learning outcomes" (para. 2). Clifford stated:
A central
strategy for developing mathematical literacy is "enabling
students to find their own independent approaches to learning" (Ulm,
2011, p. 5). Along the way, students will make mistakes and
educators must acknowledge the role that mistakes have for achieving
engagement and learning. In the view of educator Miriam Clifford (2012), "Changing
the way we see errors and the time it takes to learn can help us produce better
learning outcomes" (para. 2). Clifford stated:
According to the Ohio Department of Education (2012), there are multiple ways for developing literacy in the mathematics classroom:
Carpenter, Blanton, Cobb, Franke, Kaput, and McClain (2004) proposed that "there are four related forms of mental activity from which mathematical and scientific understanding emerges: (a) constructing relationships, (b) extending and applying mathematical and scientific knowledge, (c) justifying and explaining generalizations and procedures, and (d) developing a sense of identity related to taking responsibility for making sense of mathematical and scientific knowledge" (pp. 2-3). "Placing students' reasoning at the center of instructional decision making... represents a fundamental challenge to core educational practice" (p. 14).
According to Steve Leinwand and Steve Fleishman (2004), since the 1980s research results "consistently point to the importance of using relational practices for teaching mathematics" (p. 88). Such practices involve explaining, reasoning, and relying on multiple representations that help students develop their own understanding of content. Unfortunately, much instruction begins with instrumental practices involving memorizing and routinely applying procedures and formulas. "In existing research, students who learn rules before they learn concepts tend to score lower than do students who learn concepts first" (p. 88).
Examples:
The importance of addressing misconceptions using relational practices and multiple representations was made clear when a teacher recently voiced concern about being unable to convince a beginning algebra student that (A + B) 2 was not A2 + B2. The following visual helped clarify (A+B) (A+B) = A2 + 2AB +B2
|
A |
B |
|
|
A |
||
|
B |
|
|
This same discussion brought up a comparison to using such a visual for understanding the typical multiplication algorithm in which students have been taught to "leave off the zeroes and move each successive row of digits when multiplying left one place." Students often have no idea as to why they are doing that.
Consider the multiplication problem 31 x 25 and how the distributive property plays a role in the algorithm:
|
20 |
5 |
|
|
30 |
||
|
1 |
The visual suggests that 31 x 25 = (30 + 1)(20 + 5) = (30 x 20) + (30 x 5)+ (1 x 20) + (1 x 5) and that there will be four values (600 + 150 + 20 + 5) to add together after the products are found.
As addition can be done in any order, the above "box method" might make the transition to the traditional vertical presentation of the algorithm easier to understand, as in the following illustration:
|
|
2 |
5 |
|
2 |
5 |
|
|
2 |
5 |
|
|
|
x 3 |
1 |
|
x 3 |
1 |
|
|
x 3 |
1 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
2 |
5 |
|
|
2 |
5 |
|
|
1 |
5 |
0 |
|
|
|
|
|
|
|
|
|
6 |
0 |
0 |
7 |
5 |
0 |
|
7 |
5 |
|
|
|
7 |
7 |
5 |
7 |
7 |
5 |
|
7 |
7 |
5 |
Students at all levels benefit from a visual approach to learning mathematics. Jo Boaler (2016) and colleagues at Stanford University shared the importance of visual mathematics for the brain and learning. They indicated "when students learn through visual approaches, mathematics changes for them, and they are given access to deep and new understandings" (p. 1). Brain research has shown that "When we work on mathematics, in particular, brain activity is spread out across a widely-distributed network, which include two visual pathways: the ventral and dorsal ...Neuroimaging has shown that even when people work on a number calculation, such as 12 x 25, with symbolic digits (12 and 25) our mathematical thinking is grounded in visual processing" (p. 1).
What goes on in the classroom on a daily basis and over the course of a unit of instruction is key to processing information for understanding. Robert Marzano (2009) identified five avenues to understanding: chunking information into small bites, scaffolding, interacting, pacing, and monitoring. Of those, scaffolding is key to the entire process, as it involves the content of those chunks and their presentation in a logical order. After presenting a chunk of reasonable length, it is important for teachers to pause and allow students to interact with each other. A high rate of interaction among learners is a necessary component for understanding. Monitoring enables teachers to determine if a chunk has been understood before moving on. Pacing, how fast or slow to move through chunks, is not easily pre-determined. It depends on being able to read students' understanding and engagement with the content. The Teacher Toolkit includes over 20 tools to check for understanding throughout a lesson, including templates (e.g., 3-2-1, back and forth, buddy journal, entry ticket, exit ticket, four corners, graphic organizers, guided notes, etc.).
 In Learning in the Fast Lane: 8 Ways to
Put ALL Students on the Road to Academic Success,
Suzy Rollins (2014) noted an approach to scaffolding divided into two
categories: devices and strategies. Scaffolding devices are concrete
tools such as bookmarks, steps, flowcharts, calculators, cheat sheets,
annotations, memory devices, checklists, organizers, timelines, samples of
completed work. Scaffolding strategies are metacognitive in nature,
such as modeling, think-alouds, reciprocal teaching, and visible thinking
(p. 137). The following illustrate scaffolding devices:
In Learning in the Fast Lane: 8 Ways to
Put ALL Students on the Road to Academic Success,
Suzy Rollins (2014) noted an approach to scaffolding divided into two
categories: devices and strategies. Scaffolding devices are concrete
tools such as bookmarks, steps, flowcharts, calculators, cheat sheets,
annotations, memory devices, checklists, organizers, timelines, samples of
completed work. Scaffolding strategies are metacognitive in nature,
such as modeling, think-alouds, reciprocal teaching, and visible thinking
(p. 137). The following illustrate scaffolding devices:
Within the classroom, how teaching is organized also matters. Spacing out learning over time with review and quizzing helps learners retain information over the course of the school year and beyond. According to research, such spacing and exposure to concepts and facts should occur on at least two occasions, separated by several weeks or months. Students will learn more when teachers alternate their demonstration of a worked problem with a similar problem that students do for practice. This helps students to learn problem solving strategies, enables them to transfer those strategies more easily, and to solve problems faster. Student learning is improved if teachers connect abstract ideas and concrete contexts via stories, simulations, hands-on activities, visual representations, real-world problem solving, and so on. Teachers can also enhance learning by using higher order questioning and providing opportunities for students to develop explanations. This ranges from creating units of study that provoke question-asking and discussion to simply having students explain their thinking after solving a problem (Pashler, Bain, Bottge, et al., 2007).
 According
to the National Mathematics Advisory Panel (2008):
According
to the National Mathematics Advisory Panel (2008):
The use of “real-world” contexts to introduce mathematical ideas has been advocated, with the term “real world” being used in varied ways. A synthesis of findings from a small number of high-quality studies indicates that if mathematical ideas are taught using “real-world” contexts, then students’ performance on assessments involving similar “real-world” problems is improved. However, performance on assessments more focused on other aspects of mathematics learning, such as computation, simple word problems, and equation solving, is not improved. (p. xxiii)
Marzano, Pickering, and Pollock (2001) included nine research-based instructional strategies that have a high probability of enhancing student achievement for all students in all subject areas at all grade levels. The authors caution, however, that instructional strategies are only tools and "should not be expected to work equally well in all situations." They are grouped together into three categories for strategies that provide evidence of learning, strategies that help students acquire and integrate learning, and strategies that help students practice, review, and apply learning, as suggested by Pitler, Hubbell, and Kuhn (2012) in Using Technology with Classroom Instruction That Works:
 Strategies that provide evidence of learning:
Strategies that provide evidence of learning:
Setting objectives and providing feedback--set a unit goal and help students personalize that goal; use contracts to outline specific goals students should attain and grade they will receive if they meet those goals; use rubrics to help with feedback; provide timely, specific, and corrective feedback; consider letting students lead some feedback sessions.
Reinforcing effort and providing recognition--you might have students keep a weekly log of efforts and achievements with periodic reflections of those. They might even mathematically analyze their data. Find ways to personalize recognition, such as giving individualized awards for accomplishments.
Strategies that help students acquire and integrate learning:
Cues, questions, and advance organizers--these should be highly analytical, should focus on what is important, and are most effective when used before a learning experience.
Nonlinguistic representation--incorporate words and images using symbols to show relationships; use physical models and physical movement to represent information.
Summarizing and note taking--provide guidelines for creating a summary; give time to students to review and revise notes; use a consistent format when note taking.
Cooperative learning--consider common experiences or interests; vary group sizes and objectives. Core components include positive interdependence, group processing, appropriate use of social skills, face-to-face interaction, and individual and group accountability.
Note: Reinforcing effort from the first category also fits into this category to help students.
Strategies that help students practice, review, and apply learning:
Identifying similarities and differences (e.g., comparing, contrasting, classifying, analogies, and metaphors)-- graphic forms, such as Venn diagrams or charts, are useful.
Homework and practice--vary homework by grade level; keep parent involvement to a minimum; provide feedback on all homework; establish a homework policy; be sure students know the purpose of the homework.
Generating and testing hypotheses--a deductive (e.g. predict what might happen if ...) , rather than an inductive, approach works best.
Teaching for Understanding is a project at Harvard University that "helps educators to answer two essential questions: What does it mean to understand something? And what kinds of curricula, learning experiences, and assessment support students in developing understanding?"
 Read
Strengthening the Student Toolbox: Study Strategies to Boost Learning
by John Dunlosky (2013, Fall) in American Educator. In
Dunlosky's view, "teaching students how to learn is as important as
teaching them content, because acquiring both the right learning
strategies and background knowledge is important—if not essential—for
promoting lifelong learning" (pp. 12-13). Dunlosky noted the
following summary of the effectiveness of strategies he reviewed and
then provided tips for using effective learning strategies:
Read
Strengthening the Student Toolbox: Study Strategies to Boost Learning
by John Dunlosky (2013, Fall) in American Educator. In
Dunlosky's view, "teaching students how to learn is as important as
teaching them content, because acquiring both the right learning
strategies and background knowledge is important—if not essential—for
promoting lifelong learning" (pp. 12-13). Dunlosky noted the
following summary of the effectiveness of strategies he reviewed and
then provided tips for using effective learning strategies:
 Laney Sammons (2011) offers assistance with this endeavor in
Building Mathematical Comprehension: Using Literacy Strategies to Make Meaning. She linked reading comprehension strategies and research to mathematics
instruction. You'll find comprehension strategies for mathematics, strategies
for recognizing and understanding vocabulary, the role of schema theory and
strategies for making math connections, good questioning strategies, the
importance of visualization of mathematical ideas, and how to help learners
enhance their mathematical understanding via inferences and predictions.
There are strategies for teaching learners how to determine mathematical
importance, to synthesize for meaning and for monitoring and repairing
comprehension. Sammons also considers the components of a guided math
classroom. "This resource is aligned to the interdisciplinary themes from the Partnership for
21st Century Skills and supports the Common Core State Standards."
Laney Sammons (2011) offers assistance with this endeavor in
Building Mathematical Comprehension: Using Literacy Strategies to Make Meaning. She linked reading comprehension strategies and research to mathematics
instruction. You'll find comprehension strategies for mathematics, strategies
for recognizing and understanding vocabulary, the role of schema theory and
strategies for making math connections, good questioning strategies, the
importance of visualization of mathematical ideas, and how to help learners
enhance their mathematical understanding via inferences and predictions.
There are strategies for teaching learners how to determine mathematical
importance, to synthesize for meaning and for monitoring and repairing
comprehension. Sammons also considers the components of a guided math
classroom. "This resource is aligned to the interdisciplinary themes from the Partnership for
21st Century Skills and supports the Common Core State Standards."
 In
Teaching Students to Communicate Mathematically
Sammons (2018) provided K-8 educators with "strategies for teaching
students to express their mathematical thinking effectively—orally, with
the use of representations, and in writing. Successful literacy
strategies, including word walls, modeling, shared writing and revision,
and exemplars—strategies that show students how to talk about and write
about math" are featured (Ch. 1).
In
Teaching Students to Communicate Mathematically
Sammons (2018) provided K-8 educators with "strategies for teaching
students to express their mathematical thinking effectively—orally, with
the use of representations, and in writing. Successful literacy
strategies, including word walls, modeling, shared writing and revision,
and exemplars—strategies that show students how to talk about and write
about math" are featured (Ch. 1).
 Children's Mathematics, Second Edition: Cognitively Guided Instruction
by Thomas Carpenter, Elizabeth Fennema, Megan Franke, Linda Levi, and
Susan Empson (2014) is a go-to source to help children learn mathematics
with understanding. Per its description, highlights include:
Children's Mathematics, Second Edition: Cognitively Guided Instruction
by Thomas Carpenter, Elizabeth Fennema, Megan Franke, Linda Levi, and
Susan Empson (2014) is a go-to source to help children learn mathematics
with understanding. Per its description, highlights include:
Everything that educators do should lead to the achievement of learners. If educators are to teach for deeper learning and put research into practice, then their role also needs to change. Per Martinez, McGrath, and Foster (2016), teachers must:
The process of helping learners develop the ability to transfer knowledge to new problems and situations begins with surface learning, then moves to deep learning, and finally to transfer. John Hattie (2003) noted the following distinction between surface and deep learning:
Surface learning is more about the content (knowing the ideas, and doing what is needed to gain a passing grade), and deep learning more about understanding (relating and extending ideas, and an intention to understand and impose meaning). (p. 9)
Each stage is associated with a variety of strategies. Per Hattie and Donoghue (2016):
If the success criteria is the retention of accurate detail (surface learning) then lower-level learning strategies will be more effective than higher-level strategies. However, if the intention is to help students understand context (deeper learning) with a view to applying it in a new context (transfer), then higher level strategies are also needed. An explicit assumption is that higher level thinking requires a sufficient corpus of lower level surface knowledge to be effective—one cannot move straight to higher level thinking (e.g., problem solving and creative thought) without sufficient level of content knowledge. (Overall messages from the model section)
The National Research Council (2012) provided research-based instructional strategies focusing on deep learning:
According to Douglas Reeves (2006), "Schools that have improved achievement and closed the equity gap engage in holistic accountability, extensive nonfiction writing, frequent common assessments, decisive and immediate interventions, and constructive use of data" (p. 90). Such "accountability includes actions of adults, not merely the scores of students" (p. 83). Among those actions of adults is to assist students with gaining proficiency in a range of their own academic learning skills and behaviors. Writing in relation to the new Common Core State Standards, David Conley (2011) emphasized:
These behaviors include goal setting; study skills, both individually and in groups; self-reflection and the ability to gauge the quality of one's work; persistence with difficult tasks; a belief that effort trumps aptitude; and time-management skills. These behaviors may not be tested directly on common assessments, but without them, students are unlikely to be able to undertake complex learning tasks or take control of their own learning. (p. 20)
Assessments are not just summative, but also formative occurring at least quarterly or more with immediate feedback. Beyond a score, feedback contains detailed item and cluster analysis, and is used to inform future instruction. While individual class teachers might not be able to change student schedules to provide double classes in math or literacy for students in need, they can provide such interventions as homework supervision, break down projects into incremental steps, provide time management strategies, project management strategies, study skills, and help with reading the textbook, all of which are among immediate and decisive intervention strategies. An analysis of data in a constructive manner would reveal effective professional practices and lead to discussion on how they might be replicated (Reeves, 2006).
Educators in all instructional settings who put research into practice should apply "The Seven Principles of Good Practice in Undergraduate Education." Such practice emphasizes "active learning, time management, student-faculty contact, prompt feedback, high expectations, diverse learning styles, and cooperation among students" (Garon, 2000, para. 1). However, to reach an entire class, educators need to create an opportunity for full participation and cooperation among students.
Putting research into practice also involves building a community of learners who understand the significance of mathematics in the real-world, who can dialogue effectively about mathematics, and "do" mathematics. The following sections elaborate further on what educators can do to help achieve that goal:
 Embed
Thinking Skills within the Curriculum
Embed
Thinking Skills within the CurriculumIn 1987 Lauren Resnick noted in Education and Learning to Think that "Thinking skills resist the precise forms of definition we have come to associate with the setting of specified objectives for schooling" (p. 2). In spite of a lack of a clear definition, she noted several key features of higher-order thinking that enable one to recognize when it occurs. Higher order thinking:
Visit the National Institute of Neurological Disorders and Stroke: Brain Basics: Know Your Brain for an introduction to the brain and how it works.
 In Uncommon Sense Teaching: Practical
Insights in Brain Science to Help Students Learn, authors Barbara
Oakley, Beth Rogowsky, and Terrence Sejnowski (2021) delved into building
memory (working memory vs. long-term memory), teaching inclusively (the
importance of working memory capacity), active learning (declarative and
procedural pathways), remedies for procrastination, how human brains evolved
and why this matters for your teaching, building community through habits,
collaborative learning, lesson plans, and more. Rogowsky shared
5 Teaching Tips Using Brain Science (Ofgang, 2023, August) taken from
their book:
In Uncommon Sense Teaching: Practical
Insights in Brain Science to Help Students Learn, authors Barbara
Oakley, Beth Rogowsky, and Terrence Sejnowski (2021) delved into building
memory (working memory vs. long-term memory), teaching inclusively (the
importance of working memory capacity), active learning (declarative and
procedural pathways), remedies for procrastination, how human brains evolved
and why this matters for your teaching, building community through habits,
collaborative learning, lesson plans, and more. Rogowsky shared
5 Teaching Tips Using Brain Science (Ofgang, 2023, August) taken from
their book:
See the table of Thinking and Learning Characteristics of Young People with suggested teaching strategies, presented at PUMUS, the online journal of practical uses of math and science. The table is subdivided into sections for grades K-2, 3-5, and 6-8.
 Jay McTighe and Harvey Silver (2020) wrote
Teaching for Deeper Learning: Tools to
Engage Students in Meaning Making. They highlighted the following
seven thinking skills for the classroom that engage learners with active
meaning making leading to deeper and lasting learning:
Jay McTighe and Harvey Silver (2020) wrote
Teaching for Deeper Learning: Tools to
Engage Students in Meaning Making. They highlighted the following
seven thinking skills for the classroom that engage learners with active
meaning making leading to deeper and lasting learning:
 Peter Liljedahl
has a 14-point plan for
Building a Thinking Classroom in Math. These are briefly described in his 2017 article at
Edutopia and elaborated upon in his 2021 book
Building Thinking Classrooms in Mathematics, Grades K-12: 14 Teaching
Practices for Enhancing Learning.
Peter Liljedahl
has a 14-point plan for
Building a Thinking Classroom in Math. These are briefly described in his 2017 article at
Edutopia and elaborated upon in his 2021 book
Building Thinking Classrooms in Mathematics, Grades K-12: 14 Teaching
Practices for Enhancing Learning.
Liljedahl suggested to begin a math class with a good problem solving "thinking task" rather than direct instruction, form visibly random groups, and use vertical non-permanent surfaces (e.g., whiteboards, blackboards) on which the groups can work to solve the problem. His website, Building Thinking Classrooms, includes several BTC tasks and numeracy tasks organized by grade band.
Liljedahl also wrote Modifying Your Thinking Classroom for Different Settings: A Supplement to Building Thinking Classrooms in Mathematics (2022).
Cautionary Notes:
Although Liljedahl's instructional approach has become quite popular, not everyone agrees with it. Commenting in Don't buy into Building Thinking Classrooms in maths, it's a fad: school leader (Duggan, 2024), author and educator Dr. Greg Ashman stated, "Liljedahl’s instructional approach, designed to get students ‘thinking’, is another dangerous fad that will only misguide teachers and result in years wasted as they work to undo the damage if schools adopt it." Further, "Ashman argues the approach is deeply flawed and runs contrary to explicit teaching – the approach we know works best to build students’ mastery of new concepts." He added, "without strong foundational knowledge stored in long-term memory, novice learners will flounder in the kinds of situations BTC [Building Thinking Classrooms] creates. ... When you’ve got novices, you actually need to teach them things, not just let them get on with trying to solve problems – you actually have to teach them some strategies they can use to solve the problem…" Ashman does acknowledge that Liljedahl has done a lot of research, but "it's not effectiveness research."
 Greg Ashman is author of A Little
Guide for Teachers: Cognitive Load Theory (2023).
Greg Ashman is author of A Little
Guide for Teachers: Cognitive Load Theory (2023).
Math teacher Ryan Hooper (2024, April 11) also voiced his disagreement with Liljedahl's approach in The Math Movement Taking Over Our Schools. He noted, "The “Building Thinking Classrooms” approach defies research and common sense." He quoted from a 2006 paper by Kirschner, Sweller, and Clark, which concluded that “there is no body of research supporting the technique” and that, “not only is unguided instruction normally less effective; there is also evidence that it may have negative results when students acquire misconceptions or incomplete or disorganized knowledge.”
 The
Foundation for Critical Thinking (2019) proposed the following definition of critical thinking:
The
Foundation for Critical Thinking (2019) proposed the following definition of critical thinking:
"Critical thinking is that mode of thinking — about any subject, content, or problem — in which the thinker improves the quality of his or her thinking by skillfully analyzing, assessing, and reconstructing it. Critical thinking is self-directed, self-disciplined, self-monitored, and self-corrective thinking. It presupposes assent to rigorous standards of excellence and mindful command of their use. It entails effective communication and problem-solving abilities, as well as a commitment to overcome our native egocentrism and sociocentrism."
Teaching critical thinking is domain specific and not an easy task, but there are strategies consistent with research to help learners acquire the ability to think critically. According to Daniel Willingham (2007), a professor of cognitive psychology, "the mental activities that are typically called critical thinking are actually a subset of three types of thinking: reasoning, making judgments and decisions, and problem solving" (p. 11). Studies have revealed that:
"First, critical thinking (as well as scientific thinking and other domain-based thinking) is not a skill. There is not a set of critical thinking skills that can be acquired and deployed regardless of context. Second, there are metacognitive strategies that, once learned, make critical thinking more likely. Third, the ability to think critically (to actually do what the metacognitive strategies call for) depends on domain knowledge and practice." (p. 17)
Willingham (2019) proposed a four-step plan for teaching critical thinking:
In earlier research, Rupert Wegerif (2002) noted, the “emerging consensus, supported by some research evidence, is that the best way to teach thinking skills is not as a separate subject but through ‘infusing’ thinking skills into the teaching of content areas” (p. 3). In agreement, Willingham (2007) added that when learners "don't have much subject matter knowledge, introducing a concept by drawing on student experiences can help" (p. 18). Further, "Learners need to know what the thinking skills are that they are learning and these need to be explicitly modeled, drawn out and re-applied in different contexts. The evidence also suggests that collaborative learning improves the effectiveness of most activities" (Wegerif, 2002, p. 3).
Not only must the strategies be made explicit, but practice is an essential element. Willingham (2007) stated:
The first time (or several times) the concept is introduced, explain it with at least two different examples (possibly examples based on students’ experiences ...), label it so as to identify it as a strategy that can be applied in various contexts, and show how it applies to the course content at hand. In future instances, try naming the appropriate critical thinking strategy to see if students remember it and can figure out how it applies to the material under discussion. With still more practice, students may see which strategy applies without a cue from you. (p. 18)
Research scientists Derek Cabrera and Laura Colosi (Wheeler, 2010) identified yet another approach to teaching thinking skills, the DSRP method, that is tied to four universal patterns that structure knowledge:
DSRP focuses on making teachers and students more metacognitive and can be used in any standards-based curriculum. Cabrera and Colosi believe the system works because it is so simple.
Harvey Silver, Abigail Boutz, and Jay McTighe (2022) proposed five ideas for developing real-world thinking skills, which echo much of the thinking skills noted by Wegerif (2002). They said their IDEAS acronym for complex thinking processes reflects "how expert thinkers analyze and address real-world problems."
The value of the IDEAS acronym lies in its application as a framework for designing "rich [performance] tasks that develop complex, real-world thinking skills across grade levels and content areas" (Silver, Boutz, & McTighe, 2022).
Wegerif (2002) elaborated on each of those:
Information-processing skills: These enable pupils to locate and collect relevant information, to sort, classify, sequence, compare and contrast, and to analyze part/whole relationships.
Reasoning skills: These enable pupils to give reasons for opinions and actions, to draw inferences and make deductions, to use precise language to explain what they think, and to make judgments and decisions informed by reasons or evidence.
Enquiry skills: These enable pupils to ask relevant questions, to pose and define problems, to plan what to do and how to research, to predict outcomes and anticipate consequences, and to test conclusions and improve ideas.
Creative thinking skills: These enable pupils to generate and extend ideas, to suggest hypotheses, to apply imagination, and to look for alternative innovative outcomes.
Evaluation skills: These enable pupils to evaluate information, to judge the value of what they read, hear and do, to develop criteria for judging the value of their own and others’ work or ideas, and to have confidence in their judgments. (pp. 4-5)
Donald Treffinger (2008) distinguished between creative thinking and critical thinking, stating that effective problem solvers need both, as they are actually complementary. The former is used to generate options and the latter to focus thinking. Each form of thinking has associated guidelines and tools, illustrated in the following table.
|
Guidelines and Tools for Creative vs. Critical Thinking |
||
|
Creative |
Critical |
|
| Guidelines | Defer judgment, seek quantity, encourage all possibilities, look for new combinations that might be stronger than any of their parts. | Use affirmative judgment as opposed to being critical, be deliberate--consider the purpose of focusing, consider novelty and not only what has worked in past, stay on course. |
| Tools | Brainstorming | Hits and Hot Spots--selecting promising options and grouping in meaningful ways |
| Force-Fitting--forcing a relationship between two seemingly unrelated ideas | ALoU--acryonym for what to consider when refining and developing options: A - Advantages, L - Limitations, o - ways to overcome limitations, U - Unique features | |
| Attribute Listing | PCA or Paired Comparison Analysis--used to rank options or set priorities | |
| SCAMPER--acronym for how to apply checklist of action words to look for new possibilities: S - Substitute, C - Combine, A - Adapt, M - Magnify or Minify, P - Put to other uses, E - Eliminate, R - Reverse or Rearrange) | Sequence: SML--sequence short, medium, or long-term actions | |
| Morphological Matrix--identify key parameters of task) |
Create Evaluation Matrix-- consider all options and possibilities |
|
| Adapted from Treffinger, D. (2008, Summer). Preparing creative and critical thinkers [online]. Educational Leadership, 65(9). https://www.ascd.org/el/articles/preparing-creative-and-critical-thinkers | ||
John Spencer (2019) discussed the value of adding humor to a classroom, as humor can lead to better creative thinking. "Humor encourages creative risk-taking." It "develops divergent thinking." It "models curiosity and playfulness" and "boosts creative problem-solving." "Creative humor leads to creative fluency."
In consideration of "how expert thinkers analyze and address real-world problems" per Silver, Boutz, and McTighe (2022), there is a movement in teaching computational thinking skills and embedding those in the math curriculum.
A rationale appears to be that computational thinking is used "almost everywhere. In everyday life, at work, in school, across fields as diverse as healthcare, finance, law and music." It's "applicable to everyone" (ComputationalThinking.org).
Per ComputationalThinking.org:
"Computational thinking is a process in which you creatively apply a four-step problem-solving cycle to ideas, challenges and opportunities you encounter to develop and test solutions. The emphasis is learning how to take real-life situations and abstract—often to programs—so a computer can calculate the answer."
As in a spiral, repeat the four steps "in sequence until you reach a solution fit for the original purpose." They include:
- Define questions: Questions should be manageable to tackle. Also "Identify the information you have or will need to obtain in order to solve the problem."
- Abstract to computable form: "Transform the question into an abstract precise form, such as code, diagrams or algorithms ready for computation. Choose the concepts and tools to use to derive a solution."
- Compute answers: "Turn the abstract question into an abstract answer using the power of computation, usually with computers. Identify and resolve operational issues during the computation."
- Interpret results: "Take the abstract answer and interpret the results, recontextualising them in the scope of your original questions and sceptically verifying them. Take another turn to fix or refine."
Actually, readers should be aware that the definitioin of computational thinking has varied from researcher to researcher since the term arose (Cansu & Cansu, 2019). Readers might also conclude that the four steps above are similar to those stated in 1945 by George Polya in his Four Problem-Solving Techniques, which have become a classic for math problem-solving: understand the problem, devise a plan, carry out the plan, and look back. The difference for the computational thinking definition above is in the use of a computer to assist in problem solving.
Skills involved in computational thinking include decomposition, pattern recognition, abstraction, and algorithms. Decomposition involves breaking down a problem into smaller, manageable parts. Pattern recognition, as the name suggests, involves looking for patterns and similarities in problems. Pattern recognition is embedded in the Common Core state standards for mathematical practice in which students "Look for and make use of structure" (CCSS, 2010, MP 7). Abstraction is the process of identifying the important parts of the problem and removing extraneous information. An algorithm is developed with the step-by-step process to solve the problem. Such skills are also advocated in ISTE's Standards for Students (2024), which include that students become computational thinkers, and are reflected in its Operational Definition of Computational Thinking for K-12 Education. ISTE collaborated with the Computer Science Teachers Association on this latter definition.
ComputerBasedMath.org, a long-term project by Conrad Wolfram of Wolfram Research, is promoting computer-based math as a change in how math is taught by "using computers in school as we do in the real world: to replace humans for calculating" (What is CBM? section). You'll find a project repository that includes a collection of problems requiring computational thinking to solve. Projects are designated as beginner, intermediate, and proficient.
To learn more about thinking in the classroom, consider the following:
CueThink is one tool designed "to foster a growth mindset and empower students to see challenges as opportunities." It is presented as "an innovative application and a pedagogy focused on improving critical thinking skills and math collaboration for students in grades 2-12." This tablet and web-based product "captures and presents the thinking process and cognition." Students create a video vignette of their solutions, post to a gallery, and receive feedback from peers and their teacher, thus making math social. George Polya's four-step problem solving method is used: understand, plan, solve, and review.
The Critical Thinking Community comprises The Center for Critical Thinking and Moral Critique and the Foundation For Critical Thinking. "The work of the Foundation is to integrate the Center’s research and theoretical developments, and to create events and resources designed to help educators improve their instruction" (Mission). Resources are numerous at this site, particularly articles that define critical thinking and elaborate on the dimensions of critical thought. Articles are relevant for teaching critical thinking within the mathematics classroom.
 In
How to Teach Thinking Skills Within the Common Core, James
Bellanca, Robin Fogarty, and Brian Pete (2012)
identified three essential thinking skills for explicit teaching within
each of seven student proficiencies. Proficiencies and related skills are critical thinking (analyze, evaluate,
problem solve), creative thinking (generate, associate, hypothesize),
complex thinking (clarify, interpret, determine), comprehensive thinking
(understand, infer, compare/contrast), collaborative thinking (explain,
develop, decide), communicative thinking (reason, connect, represent), and
cognitive transfer (synthesize, generalize, apply). Such skills are
explicitly stated within the CCSS or are implicit in the language of the
standards. Each chapter includes an explicit teaching lesson, a
classroom content lesson, a CCSS performance task lesson, and reflection
questions. Online and print resources and reproducibles are also
included.
In
How to Teach Thinking Skills Within the Common Core, James
Bellanca, Robin Fogarty, and Brian Pete (2012)
identified three essential thinking skills for explicit teaching within
each of seven student proficiencies. Proficiencies and related skills are critical thinking (analyze, evaluate,
problem solve), creative thinking (generate, associate, hypothesize),
complex thinking (clarify, interpret, determine), comprehensive thinking
(understand, infer, compare/contrast), collaborative thinking (explain,
develop, decide), communicative thinking (reason, connect, represent), and
cognitive transfer (synthesize, generalize, apply). Such skills are
explicitly stated within the CCSS or are implicit in the language of the
standards. Each chapter includes an explicit teaching lesson, a
classroom content lesson, a CCSS performance task lesson, and reflection
questions. Online and print resources and reproducibles are also
included.
HOT! ISTE's Computational Thinking for All includes teacher resources, a leadership toolkit, and a video on computational thinking called "A digital age skill for everyone." With support from Google, ISTE developed "An Introduction to Computational Thinking for Every Educator," an online course for those who "want to teach students how to systematically solve problems." Also see ISTE's Resource Depository on Exploring Computational Thinking. There are over 140 resources searchable by grade bands (3-5, 6-8, 9-12) and subject, of which there are 94 for mathematics.
Learning.com: Computational Thinking for Students is included within EasyTech K-12 digital literacy curriculum. There are "over 1,000 classroom-ready lessons, activities, interactive games, and videos that help students develop a wide range of technology and computational thinking skills."
HOT!: Visible Thinking, a project at Harvard University, is a "research-based conceptual framework, which aims to integrate the development of students' thinking with content learning across subject matters" (Overview section). Of particular value is the Thinking Routine Toolbox, which "highlights thinking routines developed across a number of research projects at PZ [Harvard University's Project Zero]. A thinking routine is a set of questions or a brief sequence of steps used to scaffold and support student thinking.
Teachers who wish to develop powerful thinkers might also consider the Teaching for Robust Understanding of Mathematics (TRU Math) framework for classroom learning, which Alan Schoenfeld and colleagues at the University of California Berkeley have been developing for several years. It has been successfully applied in classrooms. The framework and supporting documents are posted at the Mathematics Assessment Project. TRU Math focuses on what students do, rather than on what teachers do, and includes five dimensions as seen below: content; cognitive demand; equitable access to content; agency, authority, and identity; and uses of assessment.
Learn more about the skills involved in computational thinking, view the YouTube video: What is Computational Thinking? The skills are explained using everyday examples.
Tech Tip: Computational Thinking is a good resource with examples on how to incorporate computational thinking in math, science, ELA, and social sciences classrooms. This resource is among many for education at The Tech Interactive.
| The Five Dimensions of Powerful Classrooms | |
| Dimension | Attributes |
| Content | The extent to which the content students engage with represents our best current disciplinary understandings (as in CCSS, NGSS, etc.). Students should have opportunities to learn important content and practices, and to develop productive disciplinary habits of mind. |
| Cognitive Demand | The extent to which classroom interactions create and maintain an environment of productive intellectual challenge conducive to students’ disciplinary development. There is a happy medium between spoon-feeding content in bite-sized pieces and having the challenges so large that students are lost at sea. |
| Equitable Access to Content | The extent to which classroom activity structures invite and support the active engagement of all of the students in the classroom with the core content being addressed by the class. No matter how rich the content being discussed, a classroom in which a small number of students get most of the “air time” is not equitable. |
| Agency, Authority, and Identity | The extent to which students have opportunities to “walk the walk and talk the talk,” building on each other’s ideas, in ways that contribute to their development of agency (the capacity and willingness to engage) and authority (recognition for being a good thinker), resulting in positive identities as thinkers and learners. |
| Uses of Assessment | The extent to which the teacher solicits student thinking and subsequent instruction responds to those ideas, by building on productive beginnings or addressing emerging misunderstandings. Powerful instruction “meets students where they are” and gives them opportunities to move forward. |
|
Source: TRU Math
at Mathematics Assessment Project. |
|
 Use Tools
and Manipulatives
Use Tools
and Manipulatives"Good mathematics teachers typically use visuals, manipulatives and motion to enhance students’ understanding of mathematical concepts, and the US national organizations for mathematics, such as the National Council for the Teaching of Mathematics (NCTM) and the Mathematical Association of America (MAA) have long advocated for the use of multiple representations in students’ learning of mathematics" (Boaler et al., 2016, p. 1).
Using appropriately tools strategically is among Common Core state standards for mathematical practice. "These tools might include pencil and paper, concrete models, a ruler, a protractor, a calculator, a spreadsheet, a computer algebra system, a statistical package, or dynamic geometry software." Further, proficient students are able to identify math resources such as "digital content located on a website and use them to pose or solve problems. They are able to use technological tools to explore and deepen their understanding of concepts" (CCSS, 2010, Math Practice MP 5).
Students' thinking and understanding will be enhanced by their use of a variety of tools. Adding to the above, include tools for visualization and analysis of mathematics such as graphic organizers, thinking maps, and both concrete and virtual manipulatives. In fact, Overall, Harold Wenglinsky (2004) concluded that "teaching that emphasizes higher-order thinking skills, project based learning, opportunities to solve problems that have multiple solutions, and such hands-on techniques as using manipulatives were all associated with higher performance on the mathematics" National Assessment of Educational Progress among 4th and 8th graders (p. 33). Using such practices to teach for meaning promotes high performance for students at all grade levels.
However, important variables to consider that influence effectiveness of tools and manipulatives (e.g., using graphic organizers) include such things as "grade level, point of implementation, instructional context, and ease of implementation" (Strangman, Vue, Hall, & Meyer, 2003, p. 10). And, there is an important caveat to using manipulatives. As the National Center on Intensive Intervention (2016) reminded educators:
"It is important to note that although students may demonstrate proper use of a manipulative, this does not mean that they understand the concepts behind use of the manipulative. Explicit instruction and student verbalizations, such as explaining the concept or demonstrating use of the manipulative while they verbally describe the mathematical procedure, should accompany all manipulative use." (p. 5)
CT4ME has an entire section devoted to math manipulatives, which includes use of calculators. Here I delve more into graphic organizers and thinking maps.
Graphic organizers and thinking maps are just two of the many methods for visualizing and analyzing. Ralph Lengler and Martin Eppler of visual-literacy.org have developed an entire Periodic Table of Visualization Methods from simple to complex.
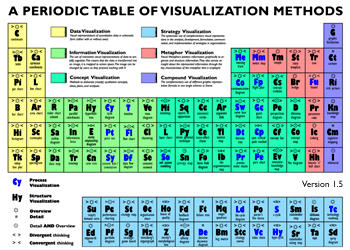
 Within the table (accessed via the link provided above), you can roll
your mouse over each element to learn more about it. You'll find
visualization methods for data, information, concepts, strategies,
metaphors, and compound use of more than one method within the same
scheme. Elements in the table also distinguish between those that
use convergent and divergent thinking, and process and structure
visualization.
Within the table (accessed via the link provided above), you can roll
your mouse over each element to learn more about it. You'll find
visualization methods for data, information, concepts, strategies,
metaphors, and compound use of more than one method within the same
scheme. Elements in the table also distinguish between those that
use convergent and divergent thinking, and process and structure
visualization.
A graphic organizer is defined as "a visual and graphic display that depicts the relationships between facts, terms, and or ideas within a learning task. Graphic organizers are also sometimes referred to as knowledge maps, concept maps, story maps, cognitive organizers, advance organizers, or concept diagrams" (Strangman, Vue, Hall, & Meyer, 2003, p. 2). They are valuable as "a creative alternative to rote memorization"; they "coincide with the brain's style of patterning" and promote this patterning "because material is presented in ways that stimulate students' brains to create meaningful and relevant connections to previously stored memories" (Willis, 2006, Ch. 1, Graphic Organizers section). They are often used in brainstorming and to help learners examine their conceptual understanding of new content.
Graphic organizers might be classified as sequential, relating to a single concept, or multiple concepts. In The Theory Underlying Concept Maps and How to Construct and Use Them, Joseph Novak and Alberto Cañas (2008) stated, concepts within a concept map are "usually enclosed in circles or boxes of some type, and relationships between concepts indicated by a connecting line linking two concepts. Words on the line, referred to as linking words or linking phrases, specify the relationship between the two concepts." Concept is defined as "a perceived regularity in events or objects, or records of events or objects, designated by a label. The label for most concepts is a word, although sometimes we use symbols such as + or %, and sometimes more than one word is used. Propositions are statements about some object or event in the universe, either naturally occurring or constructed. Propositions contain two or more concepts connected using linking words or phrases to form a meaningful statement. Sometimes these are called semantic units, or units of meaning" (Introduction section).
Concept maps are usually developed with in "a hierarchical fashion with the most inclusive, most general concepts at the top of the map and the more specific, less general concepts arranged hierarchically below." Cross-links between sub-domains on the concept map should be added, where possible, as these illustrate that learners understand interrelationships between sub-domains in the map. Specific examples illustrating or clarifying a concept can be added to the concept map, but these would not be placed within ovals or boxes, as they are not concepts (Novak & Cañas, 2008, Introduction section). Novak and Cañas presented examples of concept maps developed with CMap Tools from the Institute for Human and Machine Cognition.
Graphic organizers come in many forms. Other common forms include continuum scales, cycles of events, spider maps, Venn diagrams, compare/contrast matrices, and network tree diagrams. A Venn diagram (two or more overlapping circles) could be used to compare and contrast sets, such as in a study of least common multiple and greatest common factor, or classifying geometric shapes. A tree diagram is useful for determining outcomes in a study of probability of events, permutations and combinations. KWL charts are useful for investigations. Note: CT4ME includes KWL charts in our resource booklets for standardized test prep.
Educators might also wish to expand the KWL chart to a KWHL chart or the ultimate KWHLAQ chart to better promote 21st century skill development. These acronyms represent the following questions:
As an example, students can generate their own graphic organizer using the following sample instructions, adapted from Willis (2006, Ch. 1):
Adapted from J. Willis, Research-based strategies to ignite student learning, (2006, Ch. 1, Graphic Organizers section)
As another example, Metsisto (2005) suggested the Frayer Model and Semantic Feature Analysis Grid. The Frayer Model is used for vocabulary building and is a chart with four quadrants which can hold a definition, some characteristics/facts, examples, and non-examples of the word or concept. The word or concept might be placed at the center of the chart. The Wisconsin Department of Public Instruction includes a downloadable form for the Frayer Model that students can use.
| Frayer Model | |
| Definition |
Characteristics Facts |
|
Word or Concept |
|
| Examples | Non-Examples |
The Teacher Toolkit includes more on how to use the Frayer Model and downloadable templates.
The Semantic Feature Analysis Grid is a matrix or chart to help students to organize common features and to compare and contrast concepts. Spreadsheets are useful to design these kinds of charts. For example, Metsisto (2005) noted this grid is useful for comparing features of types of quadrilaterals.
Learn more by also reading Knowledge Maps: Tools for Building Structure in Mathematics, in which Astrid Brinkmann (2005) discussed the rules for developing mind maps and concept maps and illustrated how they are used to graphically link ideas and concepts in a well-structured form.
The following are graphic organizer web sites to consider:
Graphic Organizer Maker from Tech4Learning allows you to create custom graphic organizer worksheets for your classroom. There are multiple options from which to choose, including concept maps, KWL, KWHL, timelines, Venn diagrams, flowcharts, cycles, and more.
Graphic Organizers from Education Oasis include multiple types such as cause and effect, compare and contrast, vocabulary development, cycle of events, KWL, and more.
Graphic Organizers from EnchantedLearning.com includes multiple types with explanations of when each is used and printables.
Thinking maps are closely aligned to graphic organizers. Thinking maps are open-ended, allow students to draw on their own experience, and help them to identify, "organize, synthesize, and communicate patterns of information by using a common visual language. They enable students to explore multiple perspectives and to develop metacognitive strategies for planning, monitoring, and reflecting" (Lipton & Hyerle, n.d., p. 6). Lipton and Hyerle also described them, which I have adapted for the following table:
| Thinking Maps | ||
| Type | Purpose | Form |
| Circle | helps students generate and identify information in context related to a topic written inside the inner circle; The map might be enclosed in a square for its frame of reference. |

|
| Tree | can be used both inductively and deductively for classifying or grouping. |

|
| Bubble | can be used for describing the characteristics, qualities or attributes of something with adjectives. Any number of connecting bubbles can extend from the center. |

|
| Double-bubble | useful for comparing and contrasting. |

|
| Flow | enables students to sequence and order events, directions, cycles, and so on. |

|
| Multi-flow | helps to analyze causes and effects of an event |

|
| Brace | useful for identifying part-whole relationships of physical structures. |

|
| Bridge | helps students to interpret analogies and investigate conceptual metaphors |

|
| Adapted from Lipton, L., & Hyerle, D. (n.d.). I see what you mean: Using visual maps to assess student thinking, pp. 2-3. Thinking Foundation. https://www.eggplant.org/tf/research/journal_articles/pdf/lipton-assess-article.pdf | ||
Consider the following resource for thinking guides:
Futurelab Thinking Guides (32 page pdf) "provides a series of ready-made interactive 'thinking guides' or 'frameworks' which can support students' projects and research. Thinking guides support the thinking or working through of an issue, topic or question and help to shape, define and focus an idea and also support the planning required to investigate it further." You'll find guides to map your ideas, analyze, solve problems, explore, investigate different perspectives. You can print, edit, and share the guides with others. You can also make your own and work on them in groups.
 Incorporate Writing and Journaling in Math
Incorporate Writing and Journaling in Math

Problem solving journals and recording problem solving processes create opportunities for students to enhance their metacognition or awareness of what they are doing and why (Rhodes, 2019). As in other curricular areas, writing and journaling in math class helps students to organize and clarify their thoughts and to reflect on their understanding of concepts, or present proofs. A challenge, however, is using math vocabulary appropriately. Reeves (2006) noted, "The most effective writing is nonfiction--description, analysis, and persuasion with evidence" (p. 85). Writing includes "editing, collaborative scoring, constructive teacher feedback, and rewriting" (p. 84) in all subject areas, including math.
 Principles
and Standards for School Mathematics (NCTM, 2000) call for students to
communicate about mathematics. Writing across the grades preK-12 is
encouraged and should enable all students to--
Principles
and Standards for School Mathematics (NCTM, 2000) call for students to
communicate about mathematics. Writing across the grades preK-12 is
encouraged and should enable all students to--
NCTM's (2000) position on communication and writing about math is echoed in the Common Core Standards (2010) for Mathematical Practice, which includes that students "Construct viable arguments and critique the reasoning of others" (Standard 3). As such, teachers are changing how they teach math. According to a national survey of Common Core Math in K-8 Classrooms (Bay-Williams, Duffett, & Griffith, 2016), 64% of teachers are more often requiring students to use writing to explain their thinking and how they got their answers (p. 11).
Marilyn Burns (2004) stated that writing assignments fall into four categories: keeping journals, solving math problems, explaining concepts and ideas, and writing about learning processes. Teachers might provide initial statements, prompts, and guidelines for topics of the day for when students write to a journal. Students might write about their reasoning and problem solving process as they solve math problems. They might comment on why their solution makes sense mathematically and as a real-life solution. When explaining a concept or idea, students might also provide an example. Some writing might include commentary about the general nature of the learning activity, such as what they liked the most or least about a learning unit, or their reactions to working alone or in a group. They might show their creative side to develop a game or learning activity, or compose directions for others on how to do one of their own already-completed math activities.
To illustrate Burns' (2004) ideas, Marian Small (2010) suggested providing parallel tasks to learners as a way to differentiate math instruction. Students might choose between two problems, which differ in difficulty. However, regardless of choice, teachers might pose a set of common questions for all students to answer. Such questions focus on common elements. For example, one question might be a reflection on the estimation of the answer to the problem itself before calculating the exact answer. Another might ask students to explain why a particular operation(s) is needed to solve it, or what would happen if one number was changed, or how mental math might be used, or to explain the exact strategy actually used to solve the problem (p. 32). Students might then write answers to such questions in a journal.
Among Burns' (2004) other strategies to incorporate writing in math is to have students discuss their ideas before writing, post useful vocabulary on a class chart, and use students' writing in subsequent instruction. Posting vocabulary reminds students to use the language of math to express their ideas. Above all students should know that writing supports their learning and helps you to assess their progress. They should share their writing in pairs or small groups so that they can get alternative viewpoints or bring to light conflicting understanding. This latter provides a stringboard for further discussion.
Students need to also learn how to revise their writing. Strategies include using graphic organizers to plan writing exercises. If using paper, it is helpful to write on every other line so that there is room for revision. Reread a response to see if it makes sense and responds to the topic of the exercise.
Individuals interested in learning more about how to use writing and journaling in math classes might consult the following. You'll also find resources for products to assist with writing in math:
Improving Math and Literacy Through Writing from the Wisconsin Department of Public Instruction addresses the writing process in mathematics including writing about "text" (graphs, charts, tables, equations) in mathematics, and writing in relation to standards of mathematical processes. You'll also find a list of writing prompts for math, including how to write to stimulate "deep thinking" by using open-ended questions.
MathDL Mathematical Communication "is a developing collection of resources for engaging students in writing and speaking about mathematics, whether for the purpose of learning mathematics or of learning to communicate as mathematicians." The site addresses diverse aspects of mathematical communication, including writing as mathematicians, giving effective math presentations, talking about math to better understand it, writing about math to better understand it, communicating effectively with teammates working on a math project.
Writing about Math is a 2008 article by Wendy Petti in Education World. She noted "benefits; a variety of writing categories and topics; and suggestions for creating a positive environment for writing about math" (para. 1). Of particular interest is the list of writing prompts taken from two sources: Marvelous Math Writing Prompts, by Andrew Kaplan, Scholastic, 2001; and Standards-Based Math Graphic Organizers, Rubrics, and Writing Prompts for Middle Grade Students, by Imogene Forte and Sandra Schurr, Incentive Publications, 2001. Also of interest is the list of types of writing that can be done in math classes.
Writing to Learn Math II, a blog post (October 6, 2008) with extensive resources posted at Let's Play Math--highly recommended! It is divided into sections such as Math Journaling in General, How to get Elementary Students Writing about Math, and Journal Ideas for Older Students.
 Writing Strategies for Mathematics (Reading and Writing Strategies)
by Trisha Brummer and Stephanie Macceca (2008) is written for
learners in grades 1-8, although the strategies included can be
adapted to other grade levels. The introduction to this book
includes writing across the curriculum, motivating students to
write, and the writing process. It has three parts. Part
1: Writing to Learn Mathematics delves into learning math vocabulary
through writing, previewing and reviewing mathematics, using
journals, note-taking, using diagramming and mapping. Part 2:
Writing to Apply in Mathematics addresses authoring strategies,
summarizing, applying knowing and writing applications for
mathematics. Part 3: Assessment provides assistance with
strategies for assessing writing in mathematics. The book also
includes graphic organizers and activities with classroom examples
identified by grade ranges. Each strategy has suggestions to
help differentiate instruction.
Writing Strategies for Mathematics (Reading and Writing Strategies)
by Trisha Brummer and Stephanie Macceca (2008) is written for
learners in grades 1-8, although the strategies included can be
adapted to other grade levels. The introduction to this book
includes writing across the curriculum, motivating students to
write, and the writing process. It has three parts. Part
1: Writing to Learn Mathematics delves into learning math vocabulary
through writing, previewing and reviewing mathematics, using
journals, note-taking, using diagramming and mapping. Part 2:
Writing to Apply in Mathematics addresses authoring strategies,
summarizing, applying knowing and writing applications for
mathematics. Part 3: Assessment provides assistance with
strategies for assessing writing in mathematics. The book also
includes graphic organizers and activities with classroom examples
identified by grade ranges. Each strategy has suggestions to
help differentiate instruction.
AI NOTE: Educators have concerns about writing that might have been generated using an AI tool, such as ChatGPT, Copilot, or Bard. In 8 Ways to Create AI-Proof Writing Prompts Erik Ofgang (2024) provided the following strategies to help prevent students from submitting AI generated work:
Caution: Educators should also be aware that using ChatGPT may be eroding critical thinking skills, according to a research study at MIT's Media Lab (Chow, 2025).
 Improve
Questioning and Dialogue
Improve
Questioning and DialogueClassroom discussions and dialogue, complex problem solving, and mentoring are essential elements to help learners become critical thinkers (Goodwin, 2017). The Common Core Standards (2010) for Mathematical Practice include that students "Construct viable arguments and critique the reasoning of others" (Standard 3). In addressing this standard through questioning and dialogue, teachers facilitate interactive participation to promote their students' conceptual understanding and problem solving abilities. As students communicate with others and present their ideas, the discourse process can also help them to "Attend to precision" as they "try to use clear definitions in discussion with others and in their own reasoning" (Standard 6).
 In
Now That's a Good Question!: How to
Promote Cognitive Rigor Through Classroom Questioning, Erik Francis (2016)
proposed a Cognitive Rigor Question Framework with
eight question types and associated question stems designed to promote
cogitive rigor in the classroom. Francis noted that cognitive rigor aligns
two frameworks: Bloom's Revised Taxonomy, which "categorizes the kind of
knowledge and type of thinking that students demonstrate to answer
a question" and Webb's Depth of Knowledge, which designates the depth of
knowledge that students express in answering a question (p. 11).The
framework "categorizes questions based upon their level of complexity" (p. 149).
In
Now That's a Good Question!: How to
Promote Cognitive Rigor Through Classroom Questioning, Erik Francis (2016)
proposed a Cognitive Rigor Question Framework with
eight question types and associated question stems designed to promote
cogitive rigor in the classroom. Francis noted that cognitive rigor aligns
two frameworks: Bloom's Revised Taxonomy, which "categorizes the kind of
knowledge and type of thinking that students demonstrate to answer
a question" and Webb's Depth of Knowledge, which designates the depth of
knowledge that students express in answering a question (p. 11).The
framework "categorizes questions based upon their level of complexity" (p. 149).
In general, the National Center on Intensive Intervention (2016) noted three types of questions that should be used in mathematics to move learning forward and engage learners: reversibility, flexibility, and generalization, defined as follows:
During questioning and dialogue, both the teacher role and the students' role should be considered.
Students who feel they are valued members of the classroom will be more likely to participate in classroom discussions, particularly if they feel safe and can make an emotional and personal connection to questions that are posed. When appropriate, it's helpful if questions teachers pose also connect to student interests outside of the classroom or to other curricular areas, or real-world events.
"Participating in a mathematical community through discourse is as much a part of learning mathematics as a conceptual understanding of the mathematics itself. As students learn to make and test conjectures, question, agree, or disagree about problems, they are learning the essence of what it means to do mathematics. If all students are to be engaged, teachers must foster classroom discourse by providing a welcoming community, establishing norms, using supporting motivational discourse, and pressing for conceptual understanding." (Stein, 2007, p. 288)
Discourse standards were included among NCTM's (1991) Professional Standards for Teaching Mathematics. Teachers orchestrate discourse by "posing questions and tasks that elicit, engage, and challenge each student's thinking" (Standard 2). The art of questioning involves knowing when to listen, when to ask students to clarify and justify their ideas, when to take ideas that students present and pursue those in depth, and when and how to convert ideas into math notation. Teachers must decide when to add their own input, when to let students struggle with difficulties, and monitor and encourage participation (Standard 2). They enhance discourse with tasks that employ computers, calculators, and other technology; concrete materials used as models; pictures, diagrams, tables, and graphs; invented and conventional terms and symbols; metaphors, analogies, and stories; written hypotheses, explanations and arguments; and oral presentations and dramatizations (Standard 4).
 Mathematical discussions can involve concepts, procedures, explanations,
and various representations, which lead to a key principle that a discussion
about mathematics should achieve a goal. As not all discussions are
conducted the same way, each requires planning to achieve a particular goal.
For example, a discussion might be open-ended, if the goal was to generate
as many ideas as possible on a topic (e.g. strategies for solving a
particular problem, such as 25 x 18 mentally). Or, a discussion might
be more targeted on a particular idea. It is the teacher's role to
determine the goal, plan for how the discussion will be conducted, present
the mathematical ideas, and orient learners to how they will share ideas
with each other. It is also the teacher's role to ensure that all
learners believe their ideas are valued and that all learners contribute to
achieving the goal (Kazemi & Hintz, 2014, Ch. 1). Elham Kazemi and
Allison Hintz are authors of Intentional Talk:
How to Structure and Lead Productive Mathematical Discussions.
Mathematical discussions can involve concepts, procedures, explanations,
and various representations, which lead to a key principle that a discussion
about mathematics should achieve a goal. As not all discussions are
conducted the same way, each requires planning to achieve a particular goal.
For example, a discussion might be open-ended, if the goal was to generate
as many ideas as possible on a topic (e.g. strategies for solving a
particular problem, such as 25 x 18 mentally). Or, a discussion might
be more targeted on a particular idea. It is the teacher's role to
determine the goal, plan for how the discussion will be conducted, present
the mathematical ideas, and orient learners to how they will share ideas
with each other. It is also the teacher's role to ensure that all
learners believe their ideas are valued and that all learners contribute to
achieving the goal (Kazemi & Hintz, 2014, Ch. 1). Elham Kazemi and
Allison Hintz are authors of Intentional Talk:
How to Structure and Lead Productive Mathematical Discussions.
The process of building a community then includes what teachers say and the way they pose questions, as this affects the richness of a discussion and degree of participation. For example, asking learners "Do you have any questions?" requires only a "yes/no" response; whereas, asking "What questions do you have?" invites learners to participate. According to Paul and Elder (1997), "The oldest, and still the most powerful, teaching tactic for fostering critical thinking is Socratic teaching. In Socratic teaching we focus on giving students questions, not answers." Mastering the process of Socratic questioning is highly disciplined:
The Socratic questioner acts as the logical equivalent of the inner critical voice which the mind develops when it develops critical thinking abilities. The contributions from the members of the class are like so many thoughts in the mind. All of the thoughts must be dealt with and they must be dealt with carefully and fairly. By following up all answers with further questions, and by selecting questions which advance the discussion, the Socratic questioner forces the class to think in a disciplined, intellectually responsible manner, while yet continually aiding the students by posing facilitating questions. (Paul & Elder, 1997)
Paul and Elder (1997) noted multiple dimensions for questioning and dialogue:
We can question goals and purposes. We can probe into the nature of the question, problem, or issue that is on the floor. We can inquire into whether or not we have relevant data and information. We can consider alternative interpretations of the data and information. We can analyze key concepts and ideas. We can question assumptions being made. We can ask students to trace out the implications and consequences of what they are saying. We can consider alternative points of view. (Paul & Elder, 1997)
Teachers should "manage response rates in discussion with tiered questioning techniques." By purposefully asking "questions with ascending cognitive complexity," they will be supporting "students in deepening their thinking about content. In additon to ensuring that all student respond," teachers should "ensure that student responses are backed up by evidence," per Marzano and Toth (2014, p. 18). Providing the context for an upcoming question or setting up a hypothetical situation before posing a question about it also promotes thinking (Kelly, 2017).
Marzano (2013) found in observing teachers that their questions could be organized into four levels:
Kazemi and Hintz (2014) characterized other possible targeted discussion structures for mathematics, as noted below.
| Examples of Structures and Goals of Targeted Mathematics Discussions | |
| Targeted Discussion Structure | Goal |
| Compare and Connect | to compare similarities and differences among strategies |
| Why? Let's Justify | to generate justifications for why a particular mathematical strategy works |
| What's Best and Why? | to determine a best (most efficient) solution strategy in a particular circumstance |
| Define and Clarify | to define and discuss appropriate ways to use mathematical models, tools, vocabulary, or notation |
| Troubleshoot and Revise | to reason through which strategy produces a correct solution or figure out where a strategy when awry |
| Adapted from Kazemi, E., & Hintz, A. (2014). Intentional talk: How to structure and lead productive mathematical discussions, p. 3. Portland, ME: Stenhouse Publishers. | |
 In keeping with NCTM (1991), Margaret Smith and Mary Kay Stein (2018) provided
5 Practices
for Orchestrating Productive Mathematics Discussions (2nd edition). They include:
In keeping with NCTM (1991), Margaret Smith and Mary Kay Stein (2018) provided
5 Practices
for Orchestrating Productive Mathematics Discussions (2nd edition). They include:
Per Smith and Stein (2018), "The purpose of the five practices is to provide teachers with more control over student-centered pedagogy. They do so by allowing the teacher to manage the content that will be discussed and how it will be discussed. Through careful planning, the amount of improvisation required by the teacher “in the moment” is kept to a minimum. Thus, teachers are freed up to listen to and make sense of outlier strategies and to thoughtfully plan connections between different ways of solving problems. All of this leads to more coherent, yet student-focused, discussions" (p. 15).
However, to promote thinking and understanding for all learners, the effective questioner also needs to "draw as many students as possible into the discussion," and "periodically summarize what has and what has not been dealt with and/or resolved" (Paul & Elder, 1997). Unfortunately, this does not always occur in classrooms. Too often, math teachers tend to look for one right answer, which leads to one of the biggest problems in the art of questioning--teachers do not have an appropriate wait-time between posing the question and getting the answer. Students need time to process the question and reflect on it before answering. When there is insufficient time given, teachers tend to answer their own question, or will call on students who they are relatively certain will have that answer. Thus, the whole class is not involved.
Further, Smith and Stein (2018) promoted holding students accountable for discussion. They agree that when a question is asked, using wait-time gives students time to think and compose a response. Teachers might also ask students to restate the reasoning presented by another, or apply their own reasoning to someone else's reasoning. They might need to prompt students for further participation.
Elaborating on Smith and Stein's (2018) perspective, Matthew Kay (2022) noted "in order to lead reliably productive classroom conversations about important issues, I've got to teach good listening before anything else" (para. 2). "If the student happens to have a particular interest in the speaker's contribution, they might listen, but they don't really have to. If we want to get the most out of our classroom conversations, this quietly polite, seemingly benign disengagement must be the first unproductive habit to break" (para. 3). Teachers can "raise the bar on listening" by not just focusing on the speaker, but on what others in the class are doing at that time and encouraging students to cite each other in conversation, acknowledging that and verbally praising how well other classmates were listening. Kay found, however, that in order to cite each other, students should take notes while someone is speaking on ideas they agree or disagree with, stating that "formal citation adds academic gravity" to a discussion. Further, "Asking students to cite [classroom] conversations in graded assignments allows them to better realize that thoughtful discussion isn't a vacation from learning" (para. 7). Finally, for student conversation notes to remain meaningful, the discussion should have been focused on a big idea. Teachers should ensure that any project or activity resulting from discussion will require students to engage with that big idea. Fostering discussion citation helps students to "feel like true scholars, philosophers, and critics" (para. 9).
In his Questioning Toolkit, Jamie McKenzie listed 17 types of questions and elaborated on their role in addressing essential questions related to a unit of study. Among those are essential, organizing, elaborating, divergent, subsidiary, probing, inventive, clarification, provocative, strategic, sorting/sifting, hypothetical, planning, unanswerable, telling, irreverant, and irrelevant (McKenzie, 1997).
Unfortunately, too often teachers unskilled in the art of questioning will pose questions that involve "only simple processes like recognition, rote memory, or selective recall to formulate an answer." Such cognitive-memory questions are at the lowest level of Gallagher and Ascher's Questioning Taxonomy: cognitive-memory, convergent, divergent, and evaluative questions (Vogler, 2008, Gallagher and Ascher's Questioning Taxonomy section).
As in the online learning environment, the richest discussions will come from higher order open-ended questions (i.e., divergent or evaluative questions), as opposed to centering or closed-ended questions (i.e., cognitive-memory or convergent questions), and then probing follow-up questions (Muilenburg & Berge, 2000). Open ended questions also better involve the whole class and thus enable teachers to better differentiate instruction. Marian Small (2010) suggested four strategies on how one might do this in the mathematics classroom:
*If using the strategy to ask for similarities and differences, teachers might consider the resources provided by Sue Looney at her Same But Different Math website. She includes a series of images in multiple content areas that can be used to generate discussion. You'll find images on early numeracy, addition/subtraction, multiplication/division, measurement, place value; fractions, ratios and so on, and geometry, algebra. Teachers show two images, and pose the question "How are these images the same but different? Learners reflect alone for a couple of minutes, perhaps recording their ideas, then share ideas publicly. The next step involves the teacher to help learners to generalize a mathematical concept and summarize ideas; learners create another same but different image alone or with a partner and again share. Teachers then conclude by summarizing the ideas presented on how the images are the same but different. Per Looney, "The routine of same but different helps call attention to the features of things – and how we can connect something new to something we are already familiar with, thus helping to develop flexible gray scale thinking" (About section).
Teachers can use answers to a question to help formulate the next question, enabling questions to build upon each other. Kenneth Vogler (2008) suggested how sequencing and patterns can be accomplished:
Extending and Lifting--involves asking a series of questions (extending) at the same cognitive level, then asking a question at the next higher level (lifting).
Circular Path--ask an initial question (this one perhaps was not answered) followed by a series of questions leading back to the first one.
Same Path--all questions are asked at the same level, typically at a lower level (e.g., a series of "what is ..." questions).
Narrow to Broad--lower-level, specific questions are followed by higher-level, general questions.
Broad to Narrow--lower-level, general questions are followed by higher-level, specific questions.
A Backbone of Questions with Relevant Digressions--the series of questions relate to the topic of discussion, rather than focus on a particular cognitive level.
Art Costa and Bena Kallick (2015) sum up the art of questioning with five questions that teachers should ask themselves about the questions they pose to reach intended learning goals:
Further, when questioning learners, Berry III and Larson (2019) noted that teachers should ask themselves if they are ensuring that "all student ideas and questions are heard, valued, and pursued." They should be aware of who they call on to answer questions and whose ideas they "select for further inquiry, and whose thinking [they] tend to disregard." Teachers' questioning technique will influence how students perceive themselves, their mathematical competency, and might influence their desire to further pursue their study of mathematics (Improving instruction section).
 Caution: Sara Delano
Moore (2004) pointed out that "Many students are reluctant to ask questions
in class because they’re worried this will make them look ignorant or
they’ll be judged by their peers." It's a concern that teachers should
be aware of. To help overcome the stigma of asking questions, she
suggested implementing a "why jar" for students to anonymously submit
questions after class. They might be "Simple questions about anything
they didn’t understand in that day’s lesson or more complex questions that
would lead to a deeper discussion the next time" the class meets. If
class time runs out and some students still have questions that were not
answered, they could also add those to the jar.
Caution: Sara Delano
Moore (2004) pointed out that "Many students are reluctant to ask questions
in class because they’re worried this will make them look ignorant or
they’ll be judged by their peers." It's a concern that teachers should
be aware of. To help overcome the stigma of asking questions, she
suggested implementing a "why jar" for students to anonymously submit
questions after class. They might be "Simple questions about anything
they didn’t understand in that day’s lesson or more complex questions that
would lead to a deeper discussion the next time" the class meets. If
class time runs out and some students still have questions that were not
answered, they could also add those to the jar.
As additional resources, consider:
100 Questions that Promote Mathematical Discourse (2016) from Curriculum Associates.
Discourse resources organized by content area, including math, at Relay Graduate School of Education.
The Right Question Institute developed the Question Formation Technique (QFT), which can be used to help individuals develop better questions and participate more effectively in decisions. QFT steps involve brainstorming questions, identifying open and closed questions and discussing advantages of each type, rewriting an open question to closed and a closed question to open, prioritizing, and then investigating. The site has many resources on the questioning process.
Socratic Seminar by Daniela Castellanos-Reyes (2020) is a chapter in the e-book The Students' Guide to Learning Design and Research by R. Kimmons and S. Caskurlu. Castellanos-Reyes discusses "the Socratic Seminar as an instructional method, its historical roots, definitions, uses, and practical considerations. Readers can use this chapter as a practical guide on how to implement the Socratic Seminar in their teaching."
 Which One Doesn't Belong?
is "dedicated to providing thought-provoking puzzles for math teachers
and students alike." This site is sure to generate discussion as
each puzzle has no single correct answer. Each presents four
options for users to justify why each does not belong. Categories
include shapes, numbers, graphs and equations, and incomplete sets.
Students at all math levels, including calculus, can be challenged.
Which One Doesn't Belong?
is "dedicated to providing thought-provoking puzzles for math teachers
and students alike." This site is sure to generate discussion as
each puzzle has no single correct answer. Each presents four
options for users to justify why each does not belong. Categories
include shapes, numbers, graphs and equations, and incomplete sets.
Students at all math levels, including calculus, can be challenged.
 Likewise, students have a role in discourse per the
discourse standards
included among NCTM's (1991) Professional Standards for
Teaching Mathematics. Students:
Likewise, students have a role in discourse per the
discourse standards
included among NCTM's (1991) Professional Standards for
Teaching Mathematics. Students:
The Common Core Standards for Mathematical Practice also call for students to be able to "Construct viable arguments and critique the reasoning of others" (CCSS, 2010, Standard 3).
The art of questioning can be introduced to students as earlier as Kindergarten. When students generate their own questions, there is the potential for them to think more deeply on a topic and increase their knowledge for long-term memory. Youki Terada (2020) provided tips to help students generate productive questions in class:
The Illinois State Board of Education developed a Collaborative Learning Guide, which includes tips for creating effective collaborative activities for students working in groups or pairs to complete an assignment or task in class. It also includes management tips and a set of rules/guidelines for students to follow for respectful discussions in groups or in the classroom. There are useful sentence starters for responding to others relating to agreement, disagreement, clarifications, confirmation, confusion, extension, and review.
Joseph Manfre (2020) developed a three-part protocol meant to teach students to emphathetically explain their answers to others when they are working together and find their answers differ. He found that students might shut down their participation when others demean them for an incorrect response by saying such things as "Ha, I told you so!" He promotes heterogeneous grouping to increase opportunities for students to uncover misunderstandings and have productive discussions about those. Students need to understand that such grouping also helps to enhance their own development and motivation. His steps include:
New teachers, and some of us veterans, might have difficulty in getting students to discuss mathematics in class. You will find helpful suggestions in Effective Class Discussion at Yale University. Decentralize responses to you as teacher by encouraging learners to direct them specifically to others in the class, share discussion authority with student facilitators, ask open-ended questions, give students time to think and perhaps brainstorm answers to questions with a classmate, be encouraging to those who take risks to answer even if the answer was incorrect, use strategic body language, take notes on student responses to help summarize views later or keep discussion moving, and use active learning strategies. The Center for Research on Learning and Teaching at the University of Michigan provides a list of active learning strategies to use in the classroom.
Consider also the role that new technology tools can play in increasing dialogue about mathematics. During classtime, Marzano (2009) noted that voting options (known as clickers) often come with interactive whiteboards and "allow students to electronically cast their vote regarding the correct answer to a question. Their responses are immediately displayed on a pie chart or bar graph, enabling teacher and students to discuss the different perceptions of the correct answer" (p. 87). Technology tools can be used outside of classtime and might take the form of wikis, blogs, podcasts, or online discussion forums.
Students might use their classroom wiki to create their own textbook with group understandings of various topics, or for collaborative problem solving, projects, applications of math in everyday life, and so on. For more on the pedagogical potential of wikis, see Wiki Pedagogy posted at WikiBooks. Blogs would be useful for monitoring individual contributions of learners in discussion on a variety of topics. Their commentaries are revealed in reverse chronological order (i.e., the most recent is listed first). They might create podcasts in which they vocalize understandings individually or as a group to share with others.
Students can participate in online discussion forums. As Michael Gorman (2014) pointed out, "A discussion forum does not have to be question and answer" (online para. 2). He provided suggestions for using such forums:
Common Sense Education has several reviews on tools for online discussions. Among free tools are Kialo-edu (grades 7-12), NowComment (grades K-12), and YO Teach (grades 6-12).
For more on podcasts and blogs for learning, read articles by Patricia Deubel (2007): Podcasts: Where's the learning? and Moderating and ethics for the classroom instructional blog.
 Provide
Effective Feedback
Provide
Effective Feedback Another key to successful instruction is effective feedback and
reinforcement. However, strictly speaking, feedback is not advice, praise,
grades or evaluation, as "none of these provide the descriptive information that
students need" about their efforts to reach a goal (Wiggins, 2012, p. 11).
According to Susan Brookhart (2008) in How to Give Effective Feedback to Your Students,
feedback strategies can vary in timing (when given and how often), amount, mode (oral, written, visual/demonstration),
and audience (individual, group/class) (p. 5). It's "always adaptive.
It always depends on something else. Feedback is based on the learning
target, the particular assignment, the particular student, and the
characteristics of a given piece of work. Feedback also depends on the
depth of the teacher's understanding of the topic and of how students learn it"
(p. 112).
Another key to successful instruction is effective feedback and
reinforcement. However, strictly speaking, feedback is not advice, praise,
grades or evaluation, as "none of these provide the descriptive information that
students need" about their efforts to reach a goal (Wiggins, 2012, p. 11).
According to Susan Brookhart (2008) in How to Give Effective Feedback to Your Students,
feedback strategies can vary in timing (when given and how often), amount, mode (oral, written, visual/demonstration),
and audience (individual, group/class) (p. 5). It's "always adaptive.
It always depends on something else. Feedback is based on the learning
target, the particular assignment, the particular student, and the
characteristics of a given piece of work. Feedback also depends on the
depth of the teacher's understanding of the topic and of how students learn it"
(p. 112).
Feedback should be clearly understood, timely, immediately useable by students, consistent, comprehensive, supportive, and valued (Garon, 2000). "When anyone is trying to learn, feedback about the effort has three elements: recognition of the desired goal, evidence about present position, and some understanding of a way to close the gap between the two" (Sadler, in Black & Wiliam, 1998, Self Assessment by Pupils section).
Jan Chappuis (2012) provided the following five characteristics of effective feedback:
Everyone makes mistakes, so those who provide feedback should do so in a possitive manner, avoiding negative language. Pointing out strengths as well as weaknesses provides a balanced approach. Learners benefit from feedback tied to a rubric, as it would contain indicators of high quality work (Ntuli, 2018). Sometimes we do things that are uncharacteristic of work we might have done in past and which we might be able to correct ourselves through greater attention. So, in providing corrective feedback, we should focus on true errors, rather than pointing out all mistakes. True errors "occur because of a lack of knowledge" and fall into four broad categories," according to Douglas Fisher and Nancy Frey (2012):
David Nicol and Debra Macfarlane-Dick (2004) provided additional principles of good feedback, which are drawn from their formative assessment model and review of research literature:
Rather than limiting feedback to written forms on assignments, consider using an audio/visual format, depending on the nature of the work. Steve Kolowich (2015) noted that instructors might create short videos (2-5 minutes) with iphones or webcams, and actually take less time, on average, to do so than providing written feedback. Although some learners have reported video feedback as more personalized than written feedback, the method is not without its own drawbacks. For example, instructors need to ensure that students can easily locate/match their content to the oral statements made.
 Use Varied Instructional Approaches
Use Varied Instructional ApproachesPutting research into practice involves teaching for understanding by using a variety of instructional approaches, including technology. James Hiebert and Douglas Grouws (2009) stated that "conceptual understanding--the construction of meaningful relationships among mathematical facts, procedures, and ideas; and skill efficiency--the rapid, smooth, and accurate execution of mathematical procedures" are "central to mathematics learning and have often competed for attention" (p. 10). While teachers might wrestle with selecting effective instructional methods for increasing learning, an important point to remember is that "particular methods are not, in general, effective or ineffective. Instructional methods are effective for something" (p. 10).
Hiebert and Grouws (2009) recommended the following strategies:
For building conceptual understanding, some of time during each lesson should be spent on teachers and students explicitly talking about "relationships among facts, procedures, and ideas within a lesson and across lessons," and "the reasons why procedures work (p. 10). They should also discuss similarities and differences among different procedures that students might have used to solve problems. At least some time during the lesson, teachers should pose mathematics problems to students "just beyond what they currently know how to handle" and then have students "present their solution strategies" for class discussion" (p. 11). The idea is that understanding develops by wrestling with key math ideas and coming up with better ideas for how things work.
As to developing skill efficiency, lessons should be fast paced and should progress from the teacher's "clear and concise" modeling of new material to the group, including asking questions, to significant time for individual student practice that becomes error-free. The key is to "balance these two approaches, with a heavier emphasis on conceptual understanding" (p. 11).
Steven Ross and Deborah Lowther (2009) noted the value of using computer-assisted instruction (CAI) as a supplement to what the teacher does. Such programs can provide tutorials and "drill and practice" exercises with engaging multimedia for all learners. Effective CAI features evidence-based strategies such as adaptive content, frequent testing, and immediate feedback. CAI can also provide remedial instructioin for low-achievers, or enrichment activities, or opportunities for presenting material to students in a different way to enhance learning. If used during classtiime, it also frees the teacher to provide tutoring or time to do other classroom tasks (p. 20).
In discussing essential principles of effective math instruction for all learners, including learners with disabilities and those at risk of school failure, Karen Smith and Carol Geller (2004) said common attributes that have been identified as positively affecting student learning include:
Notice that Smith and Geller (2004) also noted the importance of feedback. In support of the above attributes, Leinwand and Fleishman (2004) suggested the following to teach for meaning:
Note: For examples on how to use open-ended problem-solving that enables learners to develop their own approaches, read Volker Ulm's (2011) Teaching mathematics - Opening up individual paths to learning.
Teachers also need to remember that varying instructional approaches is part of differentiated instruction. A mix of strategies might benefit visual, auditory, and kinesthetic learners. Visual learners appreciate lessons with graphics, illustrations, and demonstrations. Auditory learners might learn best from lectures and discussions. Kinesthetic learners process new information best when it can be touched or manipulated; thus, for this group of learners, written assignments, note taking, examination of objects, and participation in activities are valued strategies to consider.
Teachers might question if their approach should be more teacher-centered or more student-directed. The National Mathematics Advisory Panel (2008) noted, "High-quality research does not support the exclusive use of either approach" (p. 45). The terms themselves are not uniquely defined with "teacher-directed instruction ranging from highly scripted direct instruction approaches to interactive lecture styles, and with student-centered instruction ranging from students having primary responsibility for their own mathematics learning to highly structured cooperative groups" (p. 45). Ball, Ferrini-Mundy, Kilpatrick, Milgram, Schmid, and Schaar (2005) expressed:
Students can learn effectively via a mixture of direct instruction, structured investigation, and open exploration. Decisions about what is better taught through direct instruction and what might be better taught by structuring explorations for students should be made on the basis of the particular mathematics, the goals for learning, and the students' present skills and knowledge. For example, mathematical conventions and definitions should not be taught by pure discovery. Correct mathematical understanding and conclusions are the responsibility of the teacher. Making good decisions about the appropriate pedagogy to use depends on teachers having solid knowledge of the subject. (Areas of Agreement section)
It's interesting to note that direct instruction actually has different meanings. Per Rosenshine (2008) it has a general meaning and a specific meaning, and sometimes direct instruction has been viewed negatively, such as in the case of a teacher who lectures and students sit passively. He stated:
The general meaning refers to any instruction that is led by the teacher regardless of quality. However, ... the term direct instruction also has three specific uses: (a) the instructional procedures that were used by the most effective teachers [based on student achievement as found in research studies], (b) the procedures that were used in experimental studies where students were taught cognitive strategies to use in reading or writing, or (c) the instructional procedures that are used in Distar [Direct Instruction Systems in Arithmetic and Reading] classrooms. (p. 1)
There is a good deal of overlap in the three instructional meanings: Guided practice, active student participation, and fading of teacher-directed activities appear in all three meanings. Scaffolds, modeling by the teacher, and coaching of students also appear in all three. (p. 4)
This caution assumes, however, that direct instruction is being viewed as a "passive" mode of learning (Rosenshine, 2008). Students can sit and focus their attention on direct instruction only so long before they begin to tune-out. They need time to process and interact with new ideas for them to become memorable. Eric Jensen (2005) provided the following guidelines for direct instruction of new content.
| Guidelines for Direct Instruction of New Content | |
| Grade Level | Appropriate Amount of Direct Instruction |
| K-2 | 5-8 minutes |
| 3-5 | 8-12 minutes |
| 6-8 | 12-15 minutes |
| 9-12 | 12-15 minutes |
| Adult learners | 15-18 minutes |
| Source: Jensen, E. (2005). Teaching with the brain in mind (2nd ed.), p. 37. Alexandria, VA: ASCD. | |
Discovery learning is a form of partially guided instruction. Partially guided instruction is known by other names, including "problem-based learning, inquiry learning, experiential learning, and constructivist learning" (Clark, Kirschner, & Sweller, 2012, p. 7).
According to Alfieri, Brooks, Aldrich, and Tenenbaum (2011), a review of literature would suggest that "discovery learning occurs whenever the learner is not provided with the target information or conceptual understanding and must find it independently and with only the provided materials" (p. 3). The extent that assistance is provided would depend on the difficulty students might have in discovering target information. Findings in their 2011 meta-analysis of 580 comparisons of discovery learning (unassisted and assisted) and direct instruction suggested that generally "unassisted discovery does not benefit learners, whereas feedback, worked examples, scaffolding, and elicited explanations do" (p. 1). Thus, Alfieri et al. indicated the following implications for teaching:
Although direct teaching is better than unassisted discovery, providing learners with worked examples or timely feedback is preferable. ... Furthermore, [their meta-analysis suggested] teaching practices should employ scaffolded tasks that have support in place as learners attempt to reach some objective, and/or activities that require learners to explain their own ideas. The benefits of feedback, worked examples, scaffolding, and elicited explanation can be understood to be part of a more general need for learners to be redirected, to some extent, when they are mis-constructing. Feedback, scaffolding, and elicited explanations do so in more obvious ways through an interaction with the instructor, but worked examples help lead learners through problem sets in their entireties and perhaps help to promote accurate constructions as a result. (p. 12)
Per the Centre for Education Statistics and Evaluation (2017), cognitive load theory supports the use of worked examples. Researchers who have replicated the "worked example effect" have found that "novice learners who are given worked examples to study perform better on subsequent tests than learners who are required to solve the equivalent problems themselves" (p. 7). Further, "unguided problem-solving places a heavy burden on working memory, inhibiting the ability of the learner to transfer the information into their long-term memory. The learner may effectively solve the problem, but because their working memory was overloaded they may not recognise and remember the rule that would allow them to quickly solve the same problem again in the future" (p. 7). There is a caveat, however. "While cognitive load theory supports fully guided instruction for novice learners, it also supports the gradual incorporation of more independent problem-solving tasks as learners gain expertise." Worked examples might actually become less effective or redundant, as learners gain expertise (p. 7).
Richard Clark, Paul Kirschner, and John Sweller (2012) further put to rest the debate on the use of partially guided instruction. After a half century of such advocacy, "Evidence from controlled, experimental studies (a.k.a. "gold standard") almost uniformly supports full and explicit instructional guidance" (p. 11). Elaborating, they revealed:
Decades of research clearly demonstrate that for novices (comprising virtually all students), direct, explicit instruction is more effective and more efficient than partial guidance. So, when teaching new content and skills to novices, teachers are more effective when they provide explicit guidance accompanied by practice and feedback, not when they require students to discover many aspects of what they must learn. ... this does not mean direct, expository instruction all day every day. Small group and independent problems and projects can be effective--not as vehicles for making discovery, but as a means of practicing recently learned content and skills. ... Teachers providing explicit instructional guidance fully explain the concepts and skills that students are required to learn. Guidance can be provided through a variety of media, such as lectures, modeling, videos, computer-based presentations, and realistic demonstrations. It can also include class discussions and activities. (p. 6)
Kim Greene (n.d.) at Understood.org elaborated on the steps in an explicit or direct instruction lesson in How to Teach Using Explicit Instruction:
- Identify a clear, specific objective.
- Break the information into chunks.
- Model with clear explanations.
- Verbalize the thinking process.
- Provide opportunities to practive.
- Give feedback.
At Inquiry maths by Andrew Blair you will find a series of prompts that can be used in your classroom for students to explore and discuss a variety of topics. Per the website description, "Inquiry maths is a resource for a model of teaching that encourages students to regulate their own activity while exploring a mathematical statement (called a prompt). Inquiries can involve a class on diverse paths of exploration or in listening to a teacher's exposition. In inquiry maths, students take responsibility for directing the lesson with the teacher acting as the arbiter of legitimate mathematical activity." Prompts are available for number, algebra, geometry, and statistics. The site also includes an inquiry maths lesson, how to create a prompt, design an assessment for inquiry, articles, videos, and more.
Using instructional approaches such as "problem-based learning, scientific experimentation, historical investigation, Socratic seminar, research projects, problem solving, concept attainment, simulations, debates, and producing authentic products and performances" (Tomlinson & McTighe, 2006, p. 110) will help uncover the BIG ideas related to content that lie below the surface of acquiring basic skills and facts.
When teaching for understanding, a unit or course design incorporates instruction and assessment that reflects six facets of understanding. Students are provided opportunities to explain, interpret, apply, shift perspective, empathize, and self-assess (McTighe & Seif, 2002). Framing the essential or BIG questions in a unit is an important skill for educators to acquire, as these questions offer the organizing focus for a unit. Tomlinson and McTighe (2006) suggested two to five essential questions per unit, which are written at age-appropriate levels and sequenced so that one leads to the next. Students need to understand key vocabulary associated with those questions.
"Content-area concepts, thinking skills, and literacy all depend on students' abilities to use complex language" (Zwiers, O'Hara, & Pritchard, 2014, p. 6). The emphasis on vocabulary development is particularly important for learning mathematics with understanding. In mathematics, learners encounter English vocabulary that has a different meaning than when used in non-mathematics contexts (e.g., rational, negative). There's specialized vocabulary (e.g., hypotenuse, trapezoid) and terms with multiple meanings (e.g., median, base) (Kersaint, 2015).
Reading is not enough to build vocabulary. Typically learners need six exposures to new words to be able to understand, retain, and use them (Rollins, 2014, p. 79). Key vocabulary must be explicitly taught, and reinforced by posting symbols with definitions and examples to clarify meaning. Vocabulary also needs to be taught in context of use. For example, words such as power, base, product mean something entirely different in mathematics than if they would be used in other contexts.
 Marzano and Simms (2013) provided a six-step method for vocabulary instruction
in Vocabulary for the Common Core :
Marzano and Simms (2013) provided a six-step method for vocabulary instruction
in Vocabulary for the Common Core :
Rollins (2014) suggested posting a TIP (Term, Information, Picture) chart in the classroom, which would be used for reference and remain posted for the duration of a unit. It might later be used for standardized test review. Learners could also keep the TIP chart in their notebooks for personal reference. A new word is added to the chart when learners first encounter it. She cautioned against relying on dictionary definitions of vocabulary as such "definitions can be vague and contain multiple interpretations of words," which make it difficulty for learners to use those words in context. Definitions and pictures better serve learners when they are "student-friendly and collaboratively produced" (pp. 81, 85). There are other strategies to further develop vocabulary. Learners could create word art of a new term. For example, "the word circumference could scroll around a circle." Toward the middle or end of a unit, teachers could provide a list of vocabulary and ask learners, perhaps working in pairs, to determine which one does not belong. A more effective list would have multiple correct answers, thus encouraging critical thinking. Learners might also sort vocabulary or pictures associated with new terms into any number of classifications. For example, for a unit on fractions learners could sort a series of fractions into proper fractions and improper fractions, equivalent fractions, simplified fractions, or mixed numbers (pp. 86-91). In a geometry unit, they might sort angles into those that are acute, obtuse, or right angles; they might sort quadrilaterals for their features.
Consider the following resources for mathematics vocabulary:
Geneva (IL) School District 304 includes K-5 math vocabulary lists organized by grade level.
Granite School District in Salt Lake City, Utah, includes math vocabulary organized by grade level (K-8 and secondary including for the Common Core standards, and dual immersion) and resources for teaching vocabulary development.
Mathwords.com features "terms and formulas from beginning algebra to calculus." Terms include appropriate pictures, diagrams, tables, and examples and are indexed by subject area: numbers and symbols; sets, logic, proof; geometry, algebra, trigonometry, advanced algebra and precalculus, calculus, advanced topics, probability and statistics, real world applications. Entries that feature multimedia are noted.
HOT!: Virginia Department of Education Mathematics Vocabulary Word Wall Cards for grades K-8, algebra 1, geometry, algebra 2; and algebra, functions and data analysis. The "Mathematics vocabulary word wall cards provide a display of mathematics content words and associated visual cues to assist in vocabulary development." The Virginia Department of Education also indicated that the "cards should be used as an instructional tool for teachers and then as a reference for all students, particularly English learners and students with disabilities." Each list is comprehensive.
With the extent of available strategies for learning, Hattie and Donoghue (2016) provided a helpful categorization of typical strategies for moving from surface learning to deep learning and transfer, as noted in the table below.
| Learning Strategies: From Surface Learning to Deep Learning to Transfer | |
| Learning Stage | Strategies |
| Acquiring Surface Learning | record keeping, summarization, underlining and highlighting, note taking, mnemonics, outlining and transforming, organizing notes, training working memory, and imagery |
| Consolidating Surface Learning | practice testing, spaced versus mass practice, teaching test taking, interleaved practice, rehearsal, maximizing effort, help seeking, time on task, reviewing records, learning how to receive feedback and deliberate practice (i.e., practice with help of an expert, or receiving feedback during practice) |
| Acquiring Deep Learning | Self-regulation strategies include elaboration and organization, strategy monitoring, concept mapping, metacognitive strategies, self-regulation and elaborative interrogation. |
| Consolidating Deep Learning | self-verbalization, self-questioning, self-monitoring, self-explanation, self-verbalizing the steps in a problem, seeking help from peers and peer tutoring, collaborative learning, evaluation and reflection, problem solving and critical thinking techniques |
| Transfer | detecting similarities/
differences between an old and new problem or situation;
In mathematics, application of Schoenfeld's problem-solving
approach |
| Source: Hattie, J., & Donoghue, G. (2016, August). Learning strategies: A synthesis and conceptual model. npj Science of Learning, 1, 16013. doi: 10.1038/npjscilearn.2016.13. https://www.nature.com/articles/npjscilearn201613 | |
The CCSS for mathematical practice include keyword concepts such as analyze, persevere, reason, quantify, construct, critique, and model (CCSS, 2010), most of which are cognitive in nature. Per Marzano, Yanoski, Hoegh, and Simms (2013), teachers can use the following strategies, as noted in the table, to embed cognitive and conative strategies found in the ELA and mathematics practice standards. The ten cognitve strategies enable learners to complete tasks and process information. The seven conative stategies help learners to examine their knowledge and regulate their emotions and communications/interactions with others (e.g., when critiquing the reasoning of others).
| Cognitive and Conative Instructional Strategies for Addressing the Common Core ELA and Mathematical Practice Standards | |
| Cognitve Strategies* | Conative Strategies |
|
|
 Source:
Marzano, R., Yanoski, D., Hoegh, J., & Simms, J. (2013).
Using common core standards to enhance classroom instruction &
assessment. Bloomington, IN: Marzano Research Laboratory. Available:
https://amzn.to/41YFkgp Source:
Marzano, R., Yanoski, D., Hoegh, J., & Simms, J. (2013).
Using common core standards to enhance classroom instruction &
assessment. Bloomington, IN: Marzano Research Laboratory. Available:
https://amzn.to/41YFkgp*Note: The Ohio Department of Education identified five Cognitive Demand Categories for Mathematics (updated July 2024) and subskills within each category: 1. Memorize Facts, Definitions, Formulas; 2. Perform Procedures; 3. Demonstrate Understanding of Mathematical Ideas; 4. Conjecture, Analyze, Generalize, Prove; 5. Solve Non-Routine Problems / Make Connections. |
|
English language learners also benefit from materials presented in their native language, where possible. Imagine their possible confusion upon encountering homophones like "pi/pie, plane/plain, rows/rose, sine/sign, sum/some" (Bereskin, Dalrymple, Ingalls, et al., 2005, p. 3). In TIPS for English Language Learners in Mathematics, Bereskin, Dalrymple, Ingalls, and others from the Ontario (CA) Ministry of Education and their Partnership of School Boards proposed the following types of mathematical activities that help to develop both mathematics and language skills:
The Center for Applied Linguistics (CAL) recommends teachers to use the research-based Sheltered Instruction Observation Protocol (SIOP) Model in addressing the academic needs of English learners. The model "helps teachers plan and deliver lessons that allow English learners to acquire academic knowledge as they develop English language proficiency."
Stanford University has highly recommended teaching resources for Supporting ELLs in Mathematics related to the Common Core, including principles for instruction, guidelines for math instructional materials development, and "language of math" task templates (e.g., to support reading math problems, and to support math vocabulary for communication).
Visit the Teaching Channel and its K-12 Hub for free resources on instructional planning and strategies.
Ross and Lowther (2009) noted several valuable features for improving lesson quality when using
interactive whiteboards:
noted several valuable features for improving lesson quality when using
interactive whiteboards:
Further, when interactive response systems (known as clickers) are used, teachers can pose questions to students, enabling them to get immediate feedback with answers "instantly aggregated and graphically displayed" (Ross & Lowther, 2009, p. 21). This is the kind of feedback enabling timely review of lessons and student-centered community learning.
For whiteboard resources at this site, see Math Resources: Integrating Podcasts, Vodcasts and Whiteboards into Teaching and Learning.
 Teach Reading the Math Text
Teach Reading the Math Text Zwiers, O'Hara, & Pritchard (2014) reminded educators that the Common Core
Standards include that students should read and understand "complex texts"
independently and proficiently. From their work on
Common Core Standards in Diverse Classrooms:
Zwiers, O'Hara, & Pritchard (2014) reminded educators that the Common Core
Standards include that students should read and understand "complex texts"
independently and proficiently. From their work on
Common Core Standards in Diverse Classrooms:
A complex text can be any written, visual, audio, or multimedia message that conveys information or ideas for learning purposes. Complexity varies, of course. A text can be complex for some students and not complex for others. More often than not, grade-level texts in school are complex for academic English learners and others who have not been exposed to the wide ranges of ways that authors of school texts use text structure, and vocabulary to communicate their messages. (p. 63)
Hence, students should be taught how to read a math textbook. Most students, in my experience, have never learned how, and rely greatly on explanations from their teachers and jump right in to doing their homework problems without reading the text. According to Mariana Haynes (2007), "The research is clear that when teachers across content areas help students use reading comprehension strategies (such as summarizing, generating questions, and using semantic and graphic organizers), student learning improves substantially. Studies show that explicitly teaching these strategies requires students to actively process information and connect new learning with prior concepts and experiences" (p. 4).
 Reading a math text is different from reading texts in other subject areas.
In Literacy Strategies for Improving
Mathematics Instruction co-author Diana Metsisto (2005) discussed this issue in depth
in her chapter on
Reading in the Mathematics Classroom.
She stated that math texts contain a greater number of concepts per sentence and
paragraph than in texts for other subjects. Reading is complicated by the use of
numeric and non-numeric symbols, specialized vocabulary, graphics which must be
understood, page layouts that are different from other texts, and topic
sentences that often occur at the end of paragraphs instead of at the beginning.
The text is often written above the reading level of the intended learner. Some
small words when used in a math problem make a big difference in students'
understanding of a problem and how it is solved. Metsisto provided reading
strategies for math texts.
Reading a math text is different from reading texts in other subject areas.
In Literacy Strategies for Improving
Mathematics Instruction co-author Diana Metsisto (2005) discussed this issue in depth
in her chapter on
Reading in the Mathematics Classroom.
She stated that math texts contain a greater number of concepts per sentence and
paragraph than in texts for other subjects. Reading is complicated by the use of
numeric and non-numeric symbols, specialized vocabulary, graphics which must be
understood, page layouts that are different from other texts, and topic
sentences that often occur at the end of paragraphs instead of at the beginning.
The text is often written above the reading level of the intended learner. Some
small words when used in a math problem make a big difference in students'
understanding of a problem and how it is solved. Metsisto provided reading
strategies for math texts.
From their literature review on this topic, Shepherd, Selden, and Selden (2009) also indicated that "Reading mathematics often requires reading from right to left, top to bottom, bottom to top, or diagonally. ... The layout of many mathematics textbooks can make it easy to find and read worked examples while skipping crucial explanatory text" (p. 3). Learners might have difficulty with math definitions, that specialized vocabulary, if they do not understand that math definitions are "stipulated" and not the same as dictionary definitions, which are "extracted." Per Shepherd, Selden, and Selden (2009), "In a stipulated, also called an analytic, definition one must use all parts of the definition and not infer additional conditions. Such a definition can bring a concept or mathematical entity into existence. In contrast an extracted, also called a synthetic or a dictionary, definition is a description of an already existing entity. One need not use all parts of such a definition and may appropriately infer additional conditions" (p. 3).
Taking notes when reading a math textbook will also help learners become active readers and will help them to comprehend the content and raise questions for further discussion. Lent (2012) suggested two-column notes with prompts to help learners think about what they are reading. In the first column students respond to prompts appropriate to the reading selection. In the second column, students elaborate on their response or answer the question provided.
| Two-Column Notes and Prompt Ideas | |
| What is important? | What is trivial? |
| The most important sentence in this section is: | Because |
| This paragraph | Could be summarized as |
| The big idea is | The details are |
| The problem is asking me to | The most important words in this problem are |
| The concept | Looks like this (illustrate): |
| Adapted from Lent, R. C. (2012). Overcoming textbook fatigue, p. 87. Alexandria, VA: ASCD. | |
As students read a textbook, they should also have in mind questions to ask themselves. Such questions help to deepen the meaning of content, particularly when thoughts are later shared with others. Lent (2012) proposed some types:
The following are additional resources:
Cuesta College provides eight steps on How to Read A Math Textbook, referencing Winning at Math, a 1997 work by Paul D. Nolting, Ph.D.
Difficulties First-year University Students Have in Reading Their Mathematics Textbooks by Mary Shepherd, Annie Selden, and John Selden (2009). The authors conducted an exploratory study of eleven precalculus and calculus students to examine their experiences (what they do when reading) and difficulties in reading their math textbooks. Students then performed math tasks based on their reading. "Analysis of the data suggest[ed] that the reading strategies used by these students were not sufficient for them to complete many of the tasks. Instruction or guidance in strategies that are specifically related to mathematics reading may be needed to help students deal with mathematical text" (Abstract section). A value of this article also lies in the literature review on how math textbooks differ from other texts and some potential problems in reading mathematics.
How-to-study.com has tips for reading a math textbook.
Promoting Reading Strategies for Developmental Mathematics Textbooks by Anne E. Campbell, Ann Schlumberger, and Lou Ann Pate (1997) of Pima Community College presented three reading and study strategies designed to facilitate student comprehension of and learning from developmental mathematics textbooks. The discussion includes a preview, predict, read, and review reading strategy; concept cards; and a Question Answer Relationship technique. For example, concepts cards can include definitions, characteristics, examples, and nonexamples. Common kinds of concept cards in math include: (a) strategy cards for solving problems; (b) fact cards that include rules, laws, or theorems; and (c) cards for symbols and specialized vocabulary.
Reading and Writing in the Mathematics Classroom by Mark Freitag (1997) appeared in The Mathematics Educator, 8(1), 16-21. Per Freitag, the article includes "the nature of reading and writing in mathematics, list[s] some problems that students may encounter while reading or writing mathematics, and suggest[s] ways of implementing and improving reading and writing in the mathematics classroom" (p. 16).
 Provide Homework Assistance
Provide Homework AssistanceThe issue of assigning homework is controversial in terms of its purpose, what to assign, the amount of time needed to complete it, parental involvement, its actual affect on learning and achievement, and impact on family life and other valuable activities that occur outside of school hours. To help ensure that homework is completed and appropriate, consider the following research-based homework guidelines provided by Robert Marzano and Debra Pickering (2007, p. 78):
Assign purposeful homework. Legitimate purposes for homework include introducing new content, practicing a skill or process that students can do independently but not fluently, elaborating on information that has been addressed in class to deepen students' knowledge, and providing opportunities to explore topics of their own interest.
[E]nsure that homework is at the appropriate level of difficulty. Students should be able to complete homework assignments independently with relative high success rates, but they should still find the assignments challenging enough to be interesting.
Involve parents in appropriate ways (for example, as a sounding board to help students summarize what they learned from the homework) without requiring parents to act as teachers or to police students' homework completion.
Carefully monitor the amount of homework assigned so that it is appropriate to students' age levels and does not take too much time away from other home activities. (p. 78)
A rule of thumb for homework might be that "all daily homework assignments combined should take about as long to complete as 10 minutes multiplied by the students' grade level" and "when required reading is included as a type of homework, the 10-minute rule might be increased to 15 minutes" (Cooper, 2007, cited in Marzano & Pickering, 2007, p. 77).
Classroom teachers might also make learners and their parents aware of the many homework assistance sites available on the Internet, many of which are noted at CT4ME among our Math Resources: Study Skills and Homework Help.
For more on homework, including the issue of differentiated homework, read Homework: A Math Dilemma and What to Do About It (Deubel, 2007).
Back to top | Math Methodology Instruction Essay: Page 1 | 2 | 3
114th Congress of the United States. (2015). Every Student Succeeds Act. https://www.ed.gov/laws-and-policy/laws-preschool-grade-12-education/every-student-succeeds-act-essa
Alfieri, L., Brooks, P. J., Aldrich, N. J., & Tenenbaum, H. R. (2011). Does discovery-based instruction enhance learning? Journal of Educational Psychology, 103(1), 1-18. https://lexiconic.net/pedagogy/edu-103-1-1.pdf
Ball, D. L., Ferrini-Mundy, J., Kilpatrick, J., Milgram, R. J., Schmid, W., & Schaar, R. (2005). Reaching for common ground in K-12 mathematics education. Notices of the AMS, 52(9), 1055-1058. https://www.ams.org/notices/200509/comm-schmid.pdf
Bamberger, H., Oberdoff, C., & Schultz-Ferrell, K. (2010). Math misconceptions, preK-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann. https://amzn.to/48NsUu3
Bay-Williams, J., Duffett, A., & Griffith, D. (2016, June). Common core math in the K-8 classroom: Results from a national teacher survey. Washington, D.C.: Thomas B. Fordham Institute. https://fordhaminstitute.org/national/research/common-core-math-k-8-classroom-results-national-teacher-survey
Bellanca, J., Rogarty, R., & Pete, B. (2012). How to teach thinking skills within the Common Core. Bloomington, IN: Solution Tree Press. https://amzn.to/4eijz16
Bereskin, S., Dalrymple, S., Ingalls, M., et al. (2005). TIPS for English language learners in mathematics. Ontario, CA: Ministry of Education and Partnership in School Boards. https://cdnsm5-ss16.sharpschool.com/UserFiles/Servers/Server_148343/File/Programs/School%20Programs%20k-12/ESL/TIPSforELLMath4All.pdf
Berry III, R. Q., & Larson, M. R. (2019). The need to catalyze change in high school mathematics. Phi Delta Kappan, 100(6), 39-44. https://kappanonline.org/need-catalyze-change-high-school-mathematics-berry-lawson/
Black, P., & Wiliam, D. (1998). Inside the black box: Raising standards through classroom assessment [Online]. Phi Delta Kappan, 80(2), 139-144, 146-148. [Note: also see the article at https://weaeducation.typepad.co.uk/files/blackbox-1.pdf].
Boaler, J., Chen, L., Williams, C., & Cordero, M. (2016). Seeing as understanding: The importance of visual mathematics for our brain and learning. Journal of Applied & Computational Mathematics, 5(5). doi: 10.4172/2168-9679.1000325. https://www.hilarispublisher.com/open-access/seeing-as-understanding-the-importance-of-visual-mathematics-for-our-brain-and-learning-2168-9679-1000325.pdf
Booth, E. (2013). A recipe for artful schooling. Educational Leadership, 70(5), 22-27. https://www.ascd.org/el/articles/a-recipe-for-artful-schooling
Brinkmann, A. (2005, October 25). Knowledge maps: Tools for building structure in mathematics. International Journal for Mathematics Teaching and Learning. https://www.cimt.org.uk/journal/brinkmann.pdf
Brookhart, S. (2008). How to give effective feedback to your students. Alexandria, VA: ASCD. https://amzn.to/3t2th4M
Burns, M. (2004). Writing in math. Educational Leadership, 62(2), 30-33. https://www.ascd.org/el/articles/writing-in-math
Burns, M. (2014). Uncovering the math curriculum. Educational Leadership, 72(2), 64-68. https://www.ascd.org/el/articles/uncovering-the-math-curriculum
Cansu, S. K., & Cansu, F. K. (2019). An overview of computational thinking. International Journal of Computer Science Education in Schools, 3(1). https://files.eric.ed.gov/fulltext/EJ1214682.pdf
Carpenter, T. P., Blanton, M. L., Cobb, P., Franke, M. L., Kaput, J., & McClain, K. (2004). Scaling up innovative practices in mathematics and science. Madison, WI: National Center for Improving Student Learning and Achievement in Mathematics and Science. https://web.archive.org/web/20220126185617/http://greenframingham.org/stem/research/item2_scalingup_innovative_practices_math_scienceNCISLAReport1.pdf
Centre for Education Statistics and Evaluation. (2017, August). Cognitive load theory: Research that teachers really need to understand. New South Wales, Australia: Author. https://education.nsw.gov.au/about-us/educational-data/cese/publications/literature-reviews/cognitive-load-theory
Chappuis, J. (2012). "How am I doing?" Educational Leadership, 70(1), 36-40. https://www.ascd.org/el/articles/how-am-i-doing
Chow, A. (2025, June 17). ChatGPT may be eroding critical thinking skills, according to a new MIT study. Time. https://time.com/7295195/ai-chatgpt-google-learning-school/
Clark, R., Kirschner, P., & Sweller, J. (2012, Spring). Putting students on the path to learning: The case for fully guided instruction. American Educator, 36(1), 6-11. https://www.aft.org/sites/default/files/Clark.pdf
Clifford, M. (2012, November 6). The value of mistakes: Should it matter how long a student takes to learn? Open Colleges informED. https://www.opencolleges.edu.au/informed/features/the-value-of-mistakes-should-it-matter-how-long-a-student-take-to-learn/
Common Core State Standards Initiative. (2010). Common Core state standards for mathematics: Shifts in mathematics. https://www.thecorestandards.org/other-resources/key-shifts-in-mathematics/
Conley, D. T. (2011). Building on the common core. Educational Leadership, 68(6), 16-20. https://www.ascd.org/el/articles/building-on-the-common-core
Costa, A. L., & Kallick, B. (2015). Five strategies for questioning with intention. Educational Leadership, 73(1), 66-69. https://www.ascd.org/el/articles/five-strategies-for-questioning-with-intention
Deubel, P. (2007, February 21). Moderating and ethics for the classroom instructional blog. THE Journal. https://thejournal.com/articles/2007/02/21/moderating-and-ethics-for-the-classroom-instructional-blog.aspx?sc_lang=en
Deubel, P. (2007, June 7). Podcasts: Where's the learning? THE Journal. https://thejournal.com/articles/2007/06/07/podcasts-wheres-the-learning.aspx
Deubel, P. (2007, October 22). Homework: A math dilemma and what to do about it. THE Journal. https://thejournal.com/articles/2007/10/22/homework-a-math-dilemma-and-what-to-do-about-it.aspx
Duggan, S. (2024, February 20). Don't buy into Building Thinking Classrooms in maths, it's a fad: school leader. https://educationhq.com/news/dont-buy-into-building-thinking-classrooms-in-maths-its-a-fad-school-leader-166705/
Dunlosky, J. (2013, Fall). Strengthening the student toolbox: Study strategies to boost learning. American Educator, 12-21. https://www.aft.org/ae/fall2013/dunlosky
Dynarski, M. (2015, December 10). Using research to improve education under the Every Student Succeeds Act.. https://www.brookings.edu/research/using-research-to-improve-education-under-the-every-student-succeeds-act/
Ellis, K. (2005, November 8). Teaching elementary students the magic of math. Edutopia. https://www.edutopia.org/video/teaching-elementary-students-magic-math
Fisher, D., & Frey, N. (2012). Making time for feedback. Educational Leadership, 70(1), 42-47. https://www.ascd.org/el/articles/making-time-for-feedback
Francis, E. (2016). Now that's a good question!: How to promote cognitive rigor through classroom questioning. Alexandria, VA: ASCD. https://amzn.to/3sUuNWJ
Garon, J. (2000, Spring). The seven principles of effective feedback. The Law Teacher, 7(2). https://web.archive.org/web/20151004041655/http://lawteaching.org/lawteacher/2000spring/sevenprinciples.php
Goodwin, B. (2017). Research matters/ Critical thinking won't develop through osmosis. Educational Leadership, 74(5), 80-81. https://www.ascd.org/el/articles/critical-thinking-wont-develop-through-osmosis
Gorman, M. (2014, May 23). 10 tools to engage students in academic discussion forums ... Digital citizenship series. 21CenturyEdTech. https://21centuryedtech.wordpress.com/2014/05/23/10-tools-to-engage-students-in-academic-discussion-forums-digital-citizenship-series/
Greene, K. (n.d.). How to teach using explicit instruction. https://www.understood.org/en/articles/how-to-teach-using-explicit-instruction
Hattie, J. (2003, October). Teachers make a difference: What is the research evidence? Paper presented at the Australian Council for Educational Research Annual Conference on Building Teacher Quality, Melbourne. https://www.educationalleaders.govt.nz/Pedagogy-and-assessment/Building-effective-learning-environments/Teachers-Make-a-Difference-What-is-the-Research-Evidence
Hattie, J., & Donoghue, G. (2016, August). Learning strategies: a synthesis and conceptual model. npj Science of Learning, 1, 16013. doi: 10.1038/npjscilearn.2016.13. https://www.nature.com/articles/npjscilearn201613
Haynes, M. (2007, April). From state policy to classroom practice: Improving literacy instruction for all students. National Association of State Boards of Education. https://www.semanticscholar.org/paper/From-State-Policy-to-Classroom-Practice%3A-Improving-Haynes/424a2a89b15180178a0b17724360cb3e9acda1fa
Hess, F. (2021, July 5). What it takes to actually improve math education. Education Next Technology Blog. https://www.educationnext.org/what-it-takes-actually-improve-math-education-garelick/
Hewlett Foundation. (2013, April). Deeper learning defined. hthttps://hewlett.org/library/deeper-learning-defined/
Hiebert, J., & Grouws, D. (2009, Autumn). Which instructional methods are most effective for mathematics? Baltimore, MD: John Hopkins University: Better: Evidence-based Education, 2(1), 10-11. Note: A version of this article appears in Chapter 4 of Science, Technology, & Mathematics (2014) edited by Robert Slavin: https://sk.sagepub.com/dict/edvol/embed/proven-programs-in-education-science-technology-and-mathematics/chpt/which-instructional-methods-are-most-effective-mathematics
Hooper, R. (2024, April 11). The math movement taking over our schools. Education Next. https://www.educationnext.org/math-movement-taking-over-our-schools-building-thinking-classrooms/
ISTE. (2024). Standards for students. https://iste.org/standards/students
Jensen, E. (2005). Teaching with the brain in mind (2nd ed.). Alexandria, VA: ASCD. https://amzn.to/3Tbtddr
Kay, M. (2022, March 1). Classroom conversations / Listen up! A strategy for student discussions. Educational Leadership, 79(6). https://www.ascd.org/el/articles/listen-up-a-strategy-for-student-discussions
Kazemi, E., & Hintz, A. (2014). Intentional talk: How to structure and lead productive mathematical discussions. Portland, ME: Stenhouse Publishers. https://amzn.to/4a2LJuB
Kelly, M. (2017, March 8). Effective teacher questioning techniques. ThoughtCo. https://www.thoughtco.com/effective-teacher-techniques-8389
Kersaint, G. (2015, September 29). Talking math: How to engage students in mathematical discourse. https://www.gettingsmart.com/2015/09/talking-math-how-to-engage-students-in-mathematical-discourse/
Kolowich, S. (2015, January 26). Can video replace the red pen? The Chronicle of Higher Education Wired Campus Blog. https://www.chronicle.com/blogs/wiredcampus/could-video-feedback-replace-the-red-pen
Larmer, J. (2018, July 13). A tricky part of PBL: Writing a driving question [Blog post]. https://www.pblworks.org/blog/tricky-part-pbl-writing-driving-question
Leinwand, S., & Fleishman, S. (2004). Research matters / Teach mathematics right the first time. Educational Leadership, 62(1), 88-89. https://www.ascd.org/el/articles/-teach-mathematics-right-the-first-time
Lent, R. C. (2012). Overcoming textbook fatigue. Alexandria VA: ASCD. https://amzn.to/44h89GF
Lipton, L., & Hyerle, D. (n.d.). I see what you mean: Using visual maps to assess student thinking. Thinking Foundation. https://www.eggplant.org/tf/research/journal_articles/pdf/lipton-assess-article.pdf
Manfre, J. (2020, March 27). How to promote productive discussion in math. Edutopia. https://www.edutopia.org/article/how-promote-productive-discussion-math
Martinez, M., McGrath, D., & Foster, E. (2016). How deeper learning can create a new vision for teaching. Arlington, VA: National Commission on Teaching and America's Future. https://www.researchgate.net/publication/294075077_How_Deeper_Learning_Can_Create_a_New_Vision_for_Teaching
Marzano, R. (2009). Art and science of teaching / Helping students process information. Educational Leadership, 67(2), 86-87. https://www.ascd.org/el/articles/helping-students-process-information
Marzano, R. (2013). Art and science of teaching / Asking questions at four different levels. Educational Leadership, 70(5), 76-77. https://www.ascd.org/el/articles/asking-questions-at-four-different-levels
Marzano, R., & Pickering, D. (2007). Special topic / The case for and against homework. Educational Leadership, 64(6), 74-79. https://www.ascd.org/el/articles/the-case-for-and-against-homework
Marzano, R. J., Pickering, D. J., & Pollock, J. E. (2001). Classroom instruction that works (1st edition). Alexandria, VA: ASCD. https://amzn.to/4a9JCp5
Marzano, R., & Simms, J. (2013). Vocabulary for the common core (1st edition). Bloomington, IN: Marzano Research Laboratory. https://amzn.to/3ShCsrP
Marzano, R., & Toth, M. (2014). Teaching for rigor: A call for a critical instructional shift. Learning Sciences Marzano Center Monograph. West Palm Beach, FL: Learning Sciences International. https://eohighschool.com/wp-content/uploads/MC05-01-Teaching-for-Rigor-Paper-05-20-14-Digital-1-1.pdf
Marzano, R., Yanoski, D., Hoegh, J., & Simms, J. (2013). Using common core standards to enhance classroom instruction & assessment. Bloomington, IN: Marsano Research Laboratory. https://amzn.to/3GvDXfu
McKenzie, J. (1997, November/December). A questioning toolkit. From Now On, 7(3). https://web.archive.org/web/20250528023400/http://www.fno.org/nov97/toolkit.html or see https://eduscapes.com/sessions/middle/question.pdf
McTighe, J., & Seif, E. (2002). Indicators of teaching for understanding. Understanding by Design Exchange. https://edml260.pbworks.com/f/Indicators+of+teching+for+UBD.pdf
Metsisto, D. (2005). Reading in the mathematics classroom. Chapter 2 in J. M. Kenney, E. Hancewicz, L. Heuer, D. Metsisto, & C. L. Tuttle, Literacy strategies for improving mathematics instruction. Alexandria, VA: ASCD. https://amzn.to/478tdPM
Moore, S. D. (2024, December 12). How a "why jar" taught my students the value of asking questions. SmartBrief/Education. https://www.smartbrief.com/original/how-a-why-jar-taught-my-students-the-value-of-asking-questions
Morsund, D., & Ricketts, D. (2010). Math maturity. In IAE-pedia [Information Aged Education wiki]. http://web.archive.org/web/20210915131654/http://iae-pedia.org/Math_Maturity
Muilenburg, L., & Berge, Z. (2000). A framework for designing questions for online learning. The American Journal of Distance Education.. https://www.academia.edu/454284/A_Framework_for_Designing_Questions_for_Online_Learning
National Center on Intensive Intervention. (2016). Principles for designing intervention in mathematics. Washington, DC: Office of Special Education, U.S. Department of Education. https://intensiveintervention.org/resource/principles-designing-intervention-mathematics
National Council of Teachers of Mathematics. (1991). Professional Standards for Teaching Mathematics. Reston, VA: Author. https://www.nctm.org/standards/
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author. https://www.nctm.org/Standards-and-Positions/Principles-and-Standards/
National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education. https://files.eric.ed.gov/fulltext/ED500486.pdf
National Research Council. (2001). Adding it up: Helping children learn mathematics. J. Kilpatrick, J. Swafford, & B. Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press. https://www.nap.edu/catalog/9822/adding-it-up-helping-children-learn-mathematics
National Research Council. (2005). How students learn: History, science, and mathematics in the classroom. Committee on How People Learn, a targeted report for teachers, M. S. Donovan and J. D. Bransford (Eds.). Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press. https://www.nap.edu/catalog/10126/how-students-learn-history-mathematics-and-science-in-the-classroom
National Research Council. (2012, July). Education for life and work: Developing transferable knowledge and skills in the 21st century [Report Brief]. J. W. Pellegrino, & M. L. Hilton (Eds.). Committee on Defining Deeper Learning and 21st Century Skills; Center for Education; Division on Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press. https://www.nap.edu/catalog/13398/education-for-life-and-work-developing-transferable-knowledge-and-skills
Nicol, D., & Macfarlane-Dick, D. (2004). Rethinking formative assessment in HE: A theoretical model and seven principles of good feedback practice. The Higher Education Academy SENLEF Project. https://www1.villanova.edu/content/dam/villanova/vital/vitalinks/7principlesofgoodfeedback04.pdf
Novak, J. D., & A. J. Cañas, A. J. (2008). The theory underlying concept maps and how to construct them. Technical Report IHMC CmapTools 2006-01 Rev 01-2008. Florida Institute for Human and Machine Cognition. https://cmap.ihmc.us/docs/theory-of-concept-maps.php
Ntuli, E. (2018, January 11). Seven characteristics (and six tools) that support meaningful feedback. ASCD Express, 13(9). https://www.ascd.org/el/articles/seven-characteristics-(and-six-tools)-that-support-meaningful-feedback
Ofgang, E. (2023, August). 5 teaching tips using brain science. Tech & Learning. https://www.techlearning.com/news/5-teaching-tips-using-brain-science
Ofgang, E. (2024, March 18). 8 ways to create AI-proof writing prompts. Tech & Learning. https://www.techlearning.com/how-to/8-ways-to-create-ai-proof-writing-prompts
Ohio Department of Education. (2012, March 2). Ohio Mathematics Common Core Standards and Model Curriculum [YouTube video]. https://www.youtube.com/watch?v=0pJ_nI1AuLA [Note: the video is no longer available.]
Pashler, H., Bain, P., Bottge, B., Graesser, A., Koedinger, K., McDaniel, M., & Metcalfe, J. (2007). Organizing instruction and study to improve student learning (NCER 2007-2004). Washington, DC: National Center for Education Research, Institute of Education Sciences, U.S. Department of Education. https://ies.ed.gov/ncee/wwc/PracticeGuide/1
Paul, R., & Elder, L. (1997, April). Foundation for critical thinking: Socratic teaching. https://www.criticalthinking.org/pages/socratic-teaching/507
Pitler, H., Hubbell, E. R., & Kuhn, M. (2012). Using technology with classroom instruction that works (2nd edition). Alexandria, VA: ASCD. https://amzn.to/48hs8sq
Reeves, D. (2006). The learning leader: How to focus school improvement for better results (1st edition). Alexandria, VA: ASCD. https://amzn.to/417f6rM
Resnick, L. (1987). Education and learning to think. Washington, D.C.: National Academies Press. https://nap.nationalacademies.org/catalog/1032/education-and-learning-to-think
Rhodes, S. (2019, December 12). How did you solve it? Metacognition in mathematics. ASCD Express, 15(7). https://www.ascd.org/el/articles/how-did-you-solve-it-metacognition-in-mathematics
Rollins, S. P. (2014). Learning in the fast lane. Alexandria, VA: ASCD. https://amzn.to/3NfgbrA
Rosenshine, B. (2008). Five meanings of direct instruction. Lincoln, IL: Center on Innovation & Improvement. https://www.researchgate.net/publication/254957371_Five_Meanings_of_Direct_Instruction
Ross, S., & Lowther, D. (2009, Fall). Effectively using technology in education. Baltimore, MD: John Hopkins University, Better: Evidence-based Education, 20-21. Note: This article can also be found at https://www.google.com/books/edition/Proven_Programs_in_Education_Science_Tec/LgWmAwAAQBAJ?hl=en&gbpv=1&dq=Steven+Ross+and+Deborah+Lowther&pg=PA31&printsec=frontcover
Schifter, D., & Russell, S. J. (2014/2015). Beyond computation [online]. Educational Leadership, 72(4). https://www.ascd.org/el/articles/beyond-computation
Shepherd, M., Selden, A., & Selden, J. (2009). Difficulties first-year university students have in reading their mathematics textbooks. https://files.eric.ed.gov/fulltext/ED518599.pdf
Silver, H., Boutz, A., & McTighe, J. (2022). 5 ideas for developing real-world thinking skills. Educational Leadership, 79(8), 38-42. https://www.ascd.org/el/articles/5-ideas-for-developing-real-world-thinking-skills
Small, M. (2010). Beyond one right answer. Educational Leadership, 68(1), 29-32. https://www.ascd.org/el/articles/beyond-one-right-answer
Smith, K., & Geller, C. (2004). Essential principles of effective mathematics instruction: Methods to reach all students. Preventing School Failure, 48(4), 22-29. https://www.tandfonline.com/doi/abs/10.3200/PSFL.48.4.22-29
Smith, M., & Stein, M. K. (2018). 5 practices for orchestrating productive mathematics discussions (2nd edition). Reston, VA: NCTM. https://amzn.to/484OlGu
Snyder, W. (2013, August 29). Reasoning reveals and propels understanding. ASCD Express, 8(24). http://web.archive.org/web/20210123205607/http://www.ascd.org/ascd-express/vol8/824-snyder.aspx
Spencer, J. (2019, September 16). Five ways humor boosts creative thinking and problem-solving in the classroom. https://spencerauthor.com/humor-boosts-creativity/
Stein, C. (2007). Let's talk: Promoting mathematical discourse in the classroom. Mathematics Teacher, 101(4), 285-289. https://www.nctm.org/Publications/mathematics-teacher/2007/Vol101/Issue4/Let_s-Talk_-Promoting-Mathematical-Discourse-in-the-Classroom/ or https://drive.google.com/file/d/18lPR3sflbWkKKfCRPvk1lllRy9ozh4X5/view?pli=1
Strangman, N., Vue, G., Hall, T., & Meyer, A. (2003). Graphic organizers and implications for universal design for learning: Curriculum enhancement report. Wakefield, MA: National Center on Accessing the General Curriculum. (Links updated 2014). https://aem.cast.org/binaries/content/assets/common/publications/aem/ncac-graphic-organizers-udl-2014-10.docx
Terada, Y. (2020, September 24). Using student-generated questions to promote deeper thinking. Edutopia. https://www.edutopia.org/article/using-student-generated-questions-promote-deeper-thinking
The Foundation for Critical Thinking. (2019). Our concept and definition of critical thinking. https://www.criticalthinking.org/pages/our-conception-of-critical-thinking/411
Tomlinson, C., & McTighe, J. (2006). Integrating differentiated instruction & Understanding by Design. Alexandria, VA: ASCD. https://amzn.to/480Ro2p
Treffinger, D. (2008, Summer). Preparing creative and critical thinkers [online]. Educational Leadership, 65. https://www.ascd.org/el/articles/preparing-creative-and-critical-thinkers
Ulm, V. (2011). Teaching mathematics - Opening up individual paths to learning. In series: Towards New Teaching in Mathematics, Issue 3. Bayreuth, Germany: SINUS International. https://d-nb.info/1013802446/34
Vogler, K. (2008, Summer). Asking good questions [online]. Educational Leadership, 65(9). https://www.ascd.org/el/articles/asking-good-questions
Wegerif, R. (2002, September) Literature review in thinking skills, technology and learning. Futurelab Series. Bristol, UK: Futurelab. https://www.nfer.ac.uk/publications/literature-review-in-thinking-skills-technology-and-learning/
Wenglinsky, H. (2004). Facts or critical thinking skills? What NAEP results say. Educational Leadership, 62(1), 32-35. https://www.ascd.org/el/articles/facts-or-critical-thinking-skills---what-naep-results-say
Wheeler, G. (2010, August 19). A simple solution to a complex problem. ASCD Express, 5(23). http://web.archive.org/web/20210125152109/http://www.ascd.org/ascd-express/vol5/523-wheeler.aspx
Wiggins, G. (2012). Seven keys to effective feedback. Educational Leadership, 70(1), 11-16. https://www.ascd.org/el/articles/seven-keys-to-effective-feedback
Willingham, D. T. (2007, Summer). Critical thinking: Why is it so hard to teach? American Educator, 8-19. https://www.aft.org/periodical/american-educator/summer-2007/critical-thinking
Willingham, D. T. (2019). How to teach critical thinking. Education: Future Frontiers. Occasional Papers Series. https://education.nsw.gov.au/content/dam/main-education/teaching-and-learning/education-for-a-changing-world/media/documents/How-to-teach-critical-thinking-Willingham.pdf
Willis, J. (2006). Research-based strategies to ignite student learning: Insights from a neurologist and classroom teacher. Alexandria, VA: ASCD. https://amzn.to/3Rc9SXa
Wilson, D., & Conyers, M. (2016). Teaching students to drive their brains: Metacognitive strategies, activities, and lesson ideas. Alexandria, VA: ASCD. https://amzn.to/3GweeUa
Zwiers, J., O'Hara, S., & Pritchard, R. (2014). Common core standards in diverse classrooms. Portland, ME: Stenhouse Publishing. https://amzn.to/3RusP8U
![]()
Back to top | Math Methodology Instruction Essay: Page 1 | 2 | 3
![]() See
other Math Methodology pages:
See
other Math Methodology pages:
Instruction--Resources, Assessment and Curriculum: Content and Mapping